B
分析:①运用角平分线的性质及平行线的性质,易得到∠ADC+∠BCD=90°.再通过三角形的内角和为180°,求得∠CED=90°,问题得证.
②首先假设AD•BC=BE•DE成立.利用直角三角形中一条直角边所对的角对应相等,证得△BCE∽△AED,再运用相似三角形的性质证得AD•CE=BE•DE.从而得到BC=CE.与直角三角形的斜边大于一条直角边矛盾.
③在△BCE与△ECD中,利用相似三角形的判定与性质,证得CE
2=BC•CD.
④利用相似三角形的性质证得AE≠BE,使问题得证.
⑤过E作EF⊥CD与点F.通过角边角定理证得Rt△BCE≌Rt△FCE,Rt△AED≌Rt△FED.再利用全等三角形的性质证得BC=FC,AD=FD.问题得解.
解答:
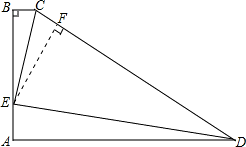
解:①∵DE平分∠ADC,CE平分∠BCD
∴∠ADE=∠CDE=

∠ADC,∠BCE=∠DCE=

∠BCD,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠ADE+∠BCE=

(∠ADC+∠BCD)=

×180°=90°,
在△CDE中,∠CED=180°-(∠ADC+∠BCD)=90°
∴DE⊥EC;
故该项成立.
②假设AD•BC=BE•DE成立.
由①知,∠CED=90°
∴∠AED+∠BEC=180°-∠CED=180°-90°=90°,
在Rt△BCE中,∠BCE+∠BEC=90°,
∴∠AED=∠BCE
∵AD∥BC,∠B=90°,
∴∠A=90°,
∴△BCE∽△AED,
∴
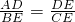
,即AD•CE=BE•DE,
∴BC=CE,
∵直角三角形的斜边>它的直角边
∴AD•BC=BE•DE不成立.
故该项不成立.
③∵CE平分∠BCD,
∴∠BCE=∠ECD,
由①知,∠CED=90°=∠B,
∴△BCE∽△ECD,
∴
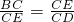
,即CE
2=BC•CD,
故该项成立.
④由②知,△BCE∽△AED,
∴
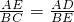
,即AE•BE=AD•BC,
显然AE≠BE,
故该选项不成立.
⑤过E作EF⊥CD与点F,
∵DE平分∠ADC,CE平分∠BCD
∴∠ADE=∠CDE,∠BCE=∠DCE,
∴Rt△BCE≌Rt△FCE,Rt△AED≌Rt△FED,
∴BC=FC,AD=FD,
又∵CF+FD=BC,
∴AD+BC=DC,
故该选项正确.
综上所述,正确的有①③⑤三个.
故选B.
点评:本题考查相似三角形的判定与性质、全等三角形的判定与性质、直角三角形的判定与性质.解决本题的关键是熟练掌握三角形全等、相似的三角形判定定理、性质定理,做到灵活运用.

 解:①∵DE平分∠ADC,CE平分∠BCD
解:①∵DE平分∠ADC,CE平分∠BCD ∠ADC,∠BCE=∠DCE=
∠ADC,∠BCE=∠DCE= ∠BCD,
∠BCD, (∠ADC+∠BCD)=
(∠ADC+∠BCD)= ×180°=90°,
×180°=90°,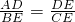 ,即AD•CE=BE•DE,
,即AD•CE=BE•DE,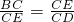 ,即CE2=BC•CD,
,即CE2=BC•CD,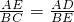 ,即AE•BE=AD•BC,
,即AE•BE=AD•BC,

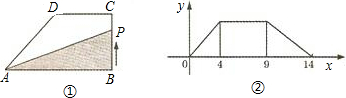
 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为