
【题目】某校学生会向全校1900名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答系列问题:
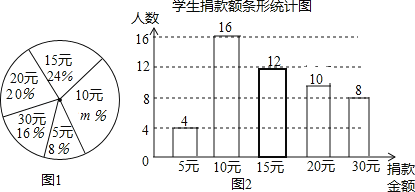
(1)本次接受随机抽样调查的学生人数为 人,图1中m的值是 .
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
【答案】(1)50,32;(2)平均数16元,众数10元,中位数15元;(3)该校本次活动捐款金额为10元的学生有608人.
【解析】
试题分析:(1)根据统计图可以分别求得本次接受随机抽样调查的学生人数和图1中m的值;
(2)根据统计图可以分别得到本次调查获取的样本数据的平均数、众数和中位数;
(3)根据统计图中的数据可以估计该校本次活动捐款金额为10元的学生人数.
解:(1)由统计图可得,
本次接受随机抽样调查的学生人数为:4÷8%=50,
m%=1﹣8%﹣16%﹣20%﹣24%=32%,
故答案为:50,32;
(2)本次调查获取的样本数据的平均数是:![]() =16(元),
=16(元),
本次调查获取的样本数据的众数是:10元,
本次调查获取的样本数据的中位数是:15元;
(3)该校本次活动捐款金额为10元的学生人数为:1900×![]() =608,
=608,
即该校本次活动捐款金额为10元的学生有608人.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.
(1)若∠ADQ=130°,求∠BED的度数;
(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).
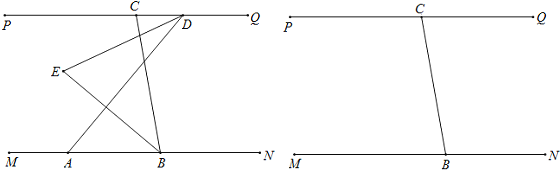
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.

解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=![]() (k>0)的图象经过点D且与边BA交于点E,连接DE.
(k>0)的图象经过点D且与边BA交于点E,连接DE.
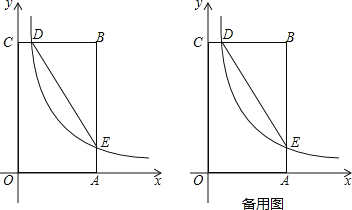
(1)连接OE,若△EOA的面积为2,则k= ;
(2)连接CA、DE与CA是否平行?请说明理由;
(3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
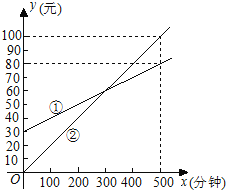
(1)有月租费的收费方式是 (填①或②),月租费是 元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com