
【题目】如图①,△ABC中, BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D.
(1)若![]() ,
,![]() ,求∠D的度数;
,求∠D的度数;
(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D、∠M、∠N的关系,并说明理由.
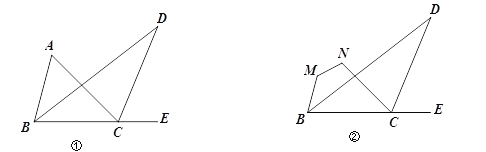
【答案】(1)![]() (2)
(2) ![]() 或写成
或写成![]()
【解析】(1).根据角平分线的定义可得∠DBC=37.5°,根据邻补角定义以及角平分线定义求得∠DCA的度数为67.5°,最后根据三角形内角和定理即可求得∠D的度数;(2).由四边形内角和与角平分线性质即可求解.
本题解析: (1)∵BD平分∠ABC,
∴∠CBD=![]() ∠ABC=
∠ABC=![]() ×75°=37.5°,
×75°=37.5°,
∵CD平分△ABC的外角,
∴∠DCA= ![]() (180°-∠ACB)=
(180°-∠ACB)= ![]() (180°-45°)=67.5°,
(180°-45°)=67.5°,
∴∠D=180°-∠DBC-∠DCB=180°-37.5°-67.5°-45°=30°;
(2) ∵∠M+∠N+∠CBM+∠NCB=360°,
∴∠D=180°-![]() ∠CBM-∠NCB-
∠CBM-∠NCB-![]() ∠NCE=180°-
∠NCE=180°-![]() (360°-∠NCB-∠M-∠N)- ∠NCB-
(360°-∠NCB-∠M-∠N)- ∠NCB-![]() ∠NCE=180°-180°+
∠NCE=180°-180°+![]() ∠NCB+
∠NCB+![]() ∠M+
∠M+![]() ∠N-∠NCB-
∠N-∠NCB-![]() ∠NCE=
∠NCE=![]() ∠M+
∠M+![]() ∠N-
∠N-![]() ∠NCB-
∠NCB-![]() ∠NCE=
∠NCE=![]() ,或写成
,或写成![]() .
.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】下列多项式乘法,不能用平方差公式计算的是( )
A.(-a-b)(-b+a)
B.(xy+z)(xy-z)
C.(-2a-b)(2a+b)
D.(0.5x-y)(-y-0.5x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC内任意一点P(a,b)经过平移后对应点P1(c,d),已知 A(3,2)在经过此次平移后对应点A1的坐标为(5,﹣1),则a+b﹣c﹣d的值为( )
A. ﹣5 B. ﹣1 C. 1 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
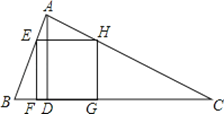
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知x1=3是关于x的一元二次方程x2-4x+c=0的一个根,求c的值和方程的另一个根.
(2)如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com