
【题目】如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:

(1)画出平移后的△A′B′C′,并直接写出点A′、B′、C′的坐标;
(2)求出在整个平移过程中,△ABC扫过的面积.
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】某蔬菜加工公司先后两批次收购蒜薹(tái)共100吨.第一批蒜薹价格为4000元/吨;因蒜薹大量上市,第二批价格跌至1000元/吨.这两批蒜薹共用去16万元.
(1)求两批次购进蒜薹各多少吨;
(2)公司收购后对蒜薹进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润1000元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向中点F,G运动.连接PB,QE,设运动时间为t(s). 
(1)求证:四边形PEQB为平行四边形;
(2)填空: ①当t=s时,四边形PBQE为菱形;
②当t=s时,四边形PBQE为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E. 
(1)求证:AC平分∠DAB;
(2)连接BE交AC于点F,若cos∠CAD= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOC=30°,∠BOC=150°,OD为∠BOA的平分线,则∠DOC=90°.若A点可表示为(2,30°),B点可表示为(4,150°),则D点可表示为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一直径是 ![]() 米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则: 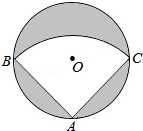
(1)AB的长为米;
(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.甲工程队施工一天,需付工程款1万元;乙工程队施工一天,需付工程款0.6万元.根据甲、乙工程队的投标书测算,可有三种施工方案:
(A)甲队单独完成这项工程,刚好如期完成;
(B)乙队单独完成这项工程要比规定工期多用4天;
(C)若甲、乙两队合做3天后,剩下的工程由乙队单独做,也正好如期完工.
为了节省工程款,同时又能如期完工,你认为应选择哪一种方案?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”。如图,在三角形ABC中,∠C=90°,较短的一条直角边BC=1,且三角形ABC是“有趣三角形”,求三角形ABC的“有趣中线”的长。
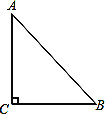
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com