
分析 (1)因为用min(a,b,c)表示这三个数中最小的数,由min{2,2x+2,4-2x}=2,得出2x+2≥2,且4-2x≥2,两个式子同时成立,据此即可求得x的范围;
(2)①M{2,x+1,2x}=$\frac{2+x+1+2x}{3}$=x+1,若M{2,x+1,2x}=min{2,x+1,2x},则x+1是2、x+1、2x中最小的一个,即:x+1≤2且x+1≤2x,据此即可求得x的值;
②根据①可以得到结论:当三个数的平均数等于三个数中的最小的数,则这几个数相等,据此即可写出;
③根据结论,三个数相等,即可求得x,y的值,从而求得x+y的值;
(3)根据二次函数图象与一次函数图象的作法作出图象,然后根据min的定义解答即可.
解答 解:(1)由min{2,2x+2,4-2x}=2,得$\left\{\begin{array}{l}{2x+2≥2}\\{4-2x≥2}\end{array}\right.$,即0≤x≤1,
故答案为:0≤x≤1;
(2)①∵M{2,x+1,2x}=min{2,x+1,2x},
∴$\left\{\begin{array}{l}{x+1≤2x}\\{x+1≤2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x≥1}\\{x≤1}\end{array}\right.$,
∴x=1;
②证明:由M{a,b,c}=min{a,b,c},可令$\frac{a+b+c}{3}$=a,即b+c=2a;
又∵$\left\{\begin{array}{l}{\frac{a+b+c}{3}≤b}\\{\frac{a+b+c}{3}≤c}\end{array}\right.$,
解之得:a+c≤2b,a+b≤2c;
把b+c=2a代入a+c≤2b 可得c≤b;把b+c=2a代入a+b≤2c可得b≤c;
∴b=c;将b=c代入b+c=2a得c=a;
∴a=b=c,
故答案为:a=b=c;
③据②可得$\left\{\begin{array}{l}{2x+y+2=x+2y}\\{2x+y+2=2x-y}\end{array}\right.$,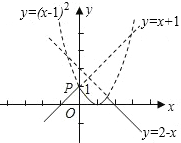
解之得y=-1,x=-3,
∴x+y=-4,
故答案为:=-4;
(3)作出图象,由图可知min{x+1,(x-1)2,2-x}的最大值为1,
故答案为:1.
点评 本题主要考查了一次函数、二次函数的图象与性质,比较大小以及利用已知提供信息得出函数值的方法,读懂题目信息并理解新定义“M”与“min”的意义是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
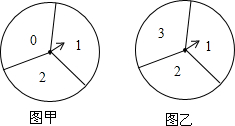 在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的,转动甲转盘,转盘停止转动后,指针所指的数字记为x,转动乙转盘,转盘停止转动后,指针所指的数字记为y,同时转动两个转盘,当转盘停止转动后,指针所指的两个数字用来表示一个点的坐标,记为(x,y),那么该点在坐标轴上的概率是$\frac{1}{3}$.
在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的,转动甲转盘,转盘停止转动后,指针所指的数字记为x,转动乙转盘,转盘停止转动后,指针所指的数字记为y,同时转动两个转盘,当转盘停止转动后,指针所指的两个数字用来表示一个点的坐标,记为(x,y),那么该点在坐标轴上的概率是$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
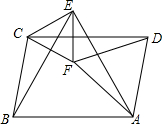 如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE、CF和EF,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上).
如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE、CF和EF,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
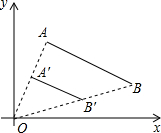 如图,线段AB的两个端点坐标分别为A(1,4),B(6,2),以原点O为位似中心,将线段AB缩小后得到线段A′B′.若AB=2A′B′,则端点B′的坐标为( )
如图,线段AB的两个端点坐标分别为A(1,4),B(6,2),以原点O为位似中心,将线段AB缩小后得到线段A′B′.若AB=2A′B′,则端点B′的坐标为( )| A. | (2,2) | B. | (3,2) | C. | (2,1) | D. | (3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
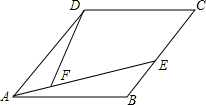 如图,四边形ABCD是菱形,点E在BC上,∠AFD=∠B,试在AE上确定一点G,使△ABG≌△DAF.请你写出两种确定点G的方案,并就其中一案的具体作法证明△ABG≌△DAF.
如图,四边形ABCD是菱形,点E在BC上,∠AFD=∠B,试在AE上确定一点G,使△ABG≌△DAF.请你写出两种确定点G的方案,并就其中一案的具体作法证明△ABG≌△DAF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
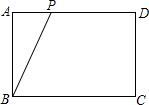 已知矩形ABCD中,AB=3cm,BC=4cm,一个动点P以1cm/s的速度从A点出发,沿AD,DC运动到C点,在这一过程中,运动时间x(s),P离D的距离为y(cm).
已知矩形ABCD中,AB=3cm,BC=4cm,一个动点P以1cm/s的速度从A点出发,沿AD,DC运动到C点,在这一过程中,运动时间x(s),P离D的距离为y(cm).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com