
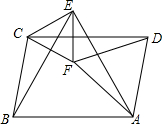
 如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE、CF和EF,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上).
如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE、CF和EF,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上).分析 根据平行四边形的对角相等,等边三角形的每一个角都是60°表示出∠CBE=∠CDF,平行四边形的对边相等,等边三角形的三条边都相等可得CB=DF,CD=BE,然后利用“边角边”证明△CDF和△EBC全等,判定①正确;同理求出△CDF和△EAF全等,根据全等三角形对应边相等可得CE=CF=EF,判定△ECF是等边三角形,判定②正确;再表示出∠EAF,可得∠CDF=∠EAF,判定③正确;根据等边三角形的性质,只有∠ABC=150°时,EF⊥CD.
解答 解:在?ABCD中,∠ADC=∠ABC,AD=BC,CD=AB,
∵△ABE、△ADF都是等边三角形,
∴AD=DF,AB=EB,∠ADF=∠ABE=60°,
∴DF=BC,CD=BC,
∴∠CDF=∠ADC-60°,
∠EBC=∠ABC-60°,
∴∠CDF=∠EBC,
在△CDF和△EBC中,$\left\{\begin{array}{l}{DF=BC}\\{∠CDF=∠EBC}\\{CD=EB}\end{array}\right.$,
∴△CDF≌△EBC(SAS),故①正确;
同理可证△CDF≌△EAF,
∴EF=CF,
∵△CDF≌△EBC,
∴CE=CF,
∴EC=CF=EF,
∴△ECF是等边三角形,故②正确;
在?ABCD中,∠DAB=180°-∠ADC,
∴∠EAF=∠DAB+∠DAF+∠BAE=180°-∠ADC+60°+60°=300°-∠ADC,
∴∠CDF=∠EAF,故③正确;
当EF⊥CD时,∵△ABE是等边三角形,
∴∠AEF=30°,
∴∠ABC=180°-30°=150°,
∵∠ABC=150°已知中没有给出,故④错误;
综上所述,正确的结论有①②③.
故答案为:①②③.
点评 本题考查了平行四边形的对边相等,邻角互补的性质,等边三角形的判定与性质,全等三角形的判定与性质,综合题但难度不大,仔细分析便不难求解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a(x+2y)(x-2y) | B. | a(x-2y)2 | C. | a(x-4y)2 | D. | a(x+4y)(x-4y) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
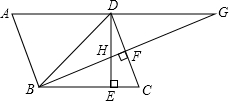 在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:
在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
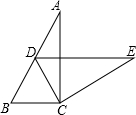 如图,在Rt△ABC中,∠ACB=90°,∠A=32°,将△ABC绕点C按顺时针方向旋转后
如图,在Rt△ABC中,∠ACB=90°,∠A=32°,将△ABC绕点C按顺时针方向旋转后查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com