
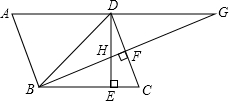
 在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:
在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①②③④ |
分析 通过判断△BDE为等腰直角三角形,得到BE=DE,BD=$\sqrt{2}$BE,则可对①进行判断;根据等角的余角相等得到∠BHE=∠C,再根据平行四边形的性质得到∠A=∠C,则∠A=∠BHE,于是可对②进行判断;由AB∥DF,得到∠ABG=90°,于是得到AB2+BG2=AG2,由等量代换可得③正确;根据三角形相似和等量代换可得④正确.
解答 解:∵∠DBC=45°,DE⊥BC,
∴△BDE为等腰直角三角形,
∴BE=DE,BD=$\sqrt{2}$BE,所以①正确;
∵BF⊥CD,
∴∠C+∠CBF=90°,
而∠BHE+∠CBF=90°,
∴∠BHE=∠C,
∵四边形ABCD为平行四边形,
∴∠A=∠C,
∴∠A=∠BHE,所以②正确;
∵AB∥DF,
∴AB⊥BG,
∴∠ABG=90°,
∴AB2+BG2=AG2,
∵AB=CD,
∴CD2+BG2=AG2;所以③正确;
∵DG∥BE,
∴△BEH∽△GDH,
∴$\frac{BE}{DG}=\frac{BH}{HG}$,
∴BH•DG=BE•HG,
∵BE=DE,
∴BH×DG=ED×GH,所以④正确;
故选D.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了平行四边形的性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
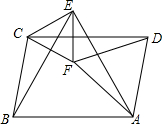 如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE、CF和EF,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上).
如图所示,在平行四边形ABCD中,分别以AB、AD为边作等边△ABE和等边△ADF,分别连接CE、CF和EF,则下列结论中一定成立的是①②③(把所有正确结论的序号都填在横线上).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
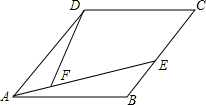 如图,四边形ABCD是菱形,点E在BC上,∠AFD=∠B,试在AE上确定一点G,使△ABG≌△DAF.请你写出两种确定点G的方案,并就其中一案的具体作法证明△ABG≌△DAF.
如图,四边形ABCD是菱形,点E在BC上,∠AFD=∠B,试在AE上确定一点G,使△ABG≌△DAF.请你写出两种确定点G的方案,并就其中一案的具体作法证明△ABG≌△DAF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
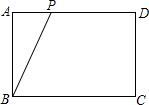 已知矩形ABCD中,AB=3cm,BC=4cm,一个动点P以1cm/s的速度从A点出发,沿AD,DC运动到C点,在这一过程中,运动时间x(s),P离D的距离为y(cm).
已知矩形ABCD中,AB=3cm,BC=4cm,一个动点P以1cm/s的速度从A点出发,沿AD,DC运动到C点,在这一过程中,运动时间x(s),P离D的距离为y(cm).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
如图,四个小正方形拼成的大正方形,A、B、O是小正方形的顶点,P是以OA为半径的⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
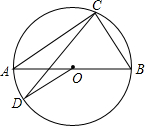 如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )
如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )| A. | 20° | B. | 30° | C. | 40° | D. | 70° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com