
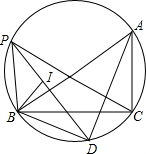
 如图,在Rt△ABC中,∠BCA=90°,∠BAC的平分线交△ABC外接圆于点D,连接BD,若AB=2AC=4.
如图,在Rt△ABC中,∠BCA=90°,∠BAC的平分线交△ABC外接圆于点D,连接BD,若AB=2AC=4.分析 (1)首先利用锐角三角函数关系得出∠BAC=60°,即可得出∠BAD=30°,进而求出BD的长即可;
(2)利用I为△CPB的内心,动点I到定点D的距离为2,即点I的轨迹是以点D为圆心,2为半径的弧CIB(不含点C、B),可求出弧CIB的长为$\frac{4}{3}$π,进而求出l的取值范围.
解答 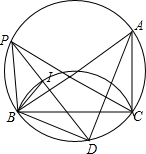 解:(1)∵∠BCA=90°,AB=2AC=4,
解:(1)∵∠BCA=90°,AB=2AC=4,
∴AC=2,则cos∠BAC=$\frac{1}{2}$,
∴∠BAC=60°,
∵∠BAC的平分线交△ABC外接圆于点D,
∴∠BAD=30°,
∴BD=$\frac{1}{2}$B=2.
故答案为:2.
(2)如图,设I为△CPB的内心,
则∠PBI=∠IBC,
∵BD=CD,
∴∠BPD=∠DBC,
∴∠PBI+∠BPD=∠IBC+∠CBD,即∠BID=∠IBD,
∴ID=BD,
∵BD=CA=2,
∴ID=2,
∴动点I到定点D的距离为2,即点I的轨迹是以点D为圆心,2为半径的弧CIB(不含点C、B),
弧CIB的长为:$\frac{120π×2}{180}$=$\frac{4π}{3}$,
则l的取值范围是:0<l<$\frac{4π}{3}$.
故答案为:0<l<$\frac{4π}{3}$.
点评 此题主要考查了圆的综合以及有关圆的性质和锐角三角函数关系、弧长公式等知识,得出$\widehat{CIB}$的长是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | 6.4的立方根是0.4 | B. | -9的平方根是±3 | ||
| C. | $\sqrt{2}$是无理数 | D. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
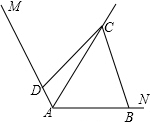 许多数学题目都有多种解法,如题目:如图,已知,∠MAN=120°,AC平分∠MAN.∠ABC+∠ADC=180°.求证:AB+AD=AC.
许多数学题目都有多种解法,如题目:如图,已知,∠MAN=120°,AC平分∠MAN.∠ABC+∠ADC=180°.求证:AB+AD=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明在大楼的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡角∠ABC=30°点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
如图,小明在大楼的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡角∠ABC=30°点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com