
【题目】(1)阅读:若一个三角形的三边长分别为a、b、c,设![]() ,
,
则这个三角形的面积为![]() .
.
(2)应用:如图1,在△ABC中,AB=6,AC=5,BC=4,求△ABC面积.
(3)引申:如图2,在(2)的条件下,AD、BE分别为△ABC的角平分线,它们的交点为I,求I到AB的距离.
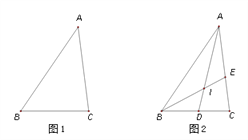
【答案】 (2) ![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:(2)先根据三边长度求出p的值,再代入公式计算可得;
(3)过点I作IF⊥AB、IG⊥AC、IH⊥BC,由角平分线性质可得IF=IH=IG,再根据S△ABC=S△ABI+S△ACI+S△BCI即可求得IF的长.
试题解析:(1)如图:
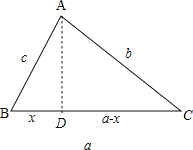
在△ABC中,过A作高AD交BC于D,
设BD=x,那么DC=a-x,
由于AD是△ABD、△ACD的公共边h2=c2-x2=b2-(a-x)2,
解出x得x=![]() ,
,
于是h=![]() ,
,
△ABC的面积S=![]() ah=
ah=![]() a
a![]()
即S=![]() a
a![]()
令p=![]() (a+b+c),
(a+b+c),
对被开方数分解因式,并整理得到s=![]() ;
;
(2)由题意,得:a=4,b=5,c=6;
∴p=![]() =
=![]() ;
;
∴S=![]() ,
,
故△ABC的面积是![]() ;
;
(3)如图,过点I作IF⊥AB、IG⊥AC、IH⊥BC,垂足分别为点F、G、H,
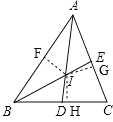
∵AD、BE分别为△ABC的角平分线,
∴IF=IH=IG,
∵S△ABC=S△ABI+S△ACI+S△BCI,
即![]() ,
,
∴3IF+![]() IF+2IF=
IF+2IF=![]() ,
,
解得IF=![]() ,
,
故I到AB的距离为![]() .
.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
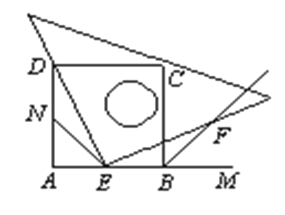
【题目】如图所示,四边形ABCD是正方形,M是AB延长线上一点。直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F。
⑴如图1,当点E在AB边的中点位置时:
①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是 ;
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ;
⑵请你证明上述两种猜想?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身份证号码告诉我们很多信息,某人的身份证号码130503196704010012,其中13、05、03是此人所属的省(市、自治区)、市、县(市、区)的编码,1967、04、01是此人出生的年、月、日,001是顺序码,2为校验码.那么身份证号码是321084198101208022的人的生日是( )
A. 8月10日 B. 10月12日 C. 1月20日 D. 12月8日
查看答案和解析>>
科目:初中数学 来源: 题型:
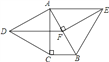
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当![]() =____时,四边形ADFE是平行四边形.
=____时,四边形ADFE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
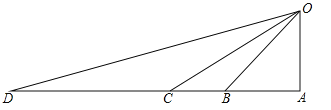
【题目】“一号龙卷风”给小岛O造成了较大的破坏,救灾部门迅速组织力量,从仓储D处调集救援物资,计划先用汽车运到与D在同一直线上的C、B、A三个码头中的一处,再用货船运到小岛O.已知:OA⊥AD,∠ODA=15°,∠OCA=30°,∠OBA=45°CD=20km.若汽车行驶的速度为50km/时,货船航行的速度为25km/时,问这批物资在哪个码头装船,最早运抵小岛O?(在物资搬运能力上每个码头工作效率相同,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7).
≈1.7).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com