
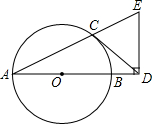
 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.分析 (1)利用切线的性质结合等腰三角形的性质得出∠DCE=∠E,进而得出答案;
(2)设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,利用勾股定理得出BD的长.
解答 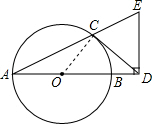 (1)证明:连接OC,
(1)证明:连接OC,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ACO+∠DCE=90°,
又∵ED⊥AD,∴∠EDA=90°,
∴∠EAD+∠E=90°,
∵OC=OA,∴∠ACO=∠EAD,
故∠DCE=∠E,
∴DC=DE,
(2)解:设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,
在Rt△EAD中,
∵tan∠CAB=$\frac{1}{2}$,∴ED=$\frac{1}{2}$AD=$\frac{1}{2}$(3+x),
由(1)知,DC=$\frac{1}{2}$(3+x),在Rt△OCD中,
OC2+CD2=DO2,
则1.52+[$\frac{1}{2}$(3+x)]2=(1.5+x)2,
解得:x1=-3(舍去),x2=1,
故BD=1.
点评 此题主要考查了切线的性质以及以及勾股定理和等腰三角形的性质等知识,熟练应用切线的性质得出∠OCD=90°是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
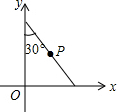 如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )| A. | ($\sqrt{3}$,1) | B. | (1,-$\sqrt{3}$) | C. | (2$\sqrt{3}$,-2) | D. | (2,-2$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com