
【题目】如图,△ABC的中线AE,BD交于点G,过点D作DM∥BC交AE于点M,则△AMD,△DMG和△BEG的面积之比为 . 
【答案】3:1:4
【解析】解:∵线段AE、BD是△ABC的中线,
∴BE=CE,AD=CD,
∵DM∥BC,
∴AM=ME,
∴DM= ![]() CE=
CE= ![]() BE,
BE,
∵DM∥BC,
∴△DMG∽△BEG,
∴ ![]() =
= ![]() ,S△BGE:S△DMG=4:1,
,S△BGE:S△DMG=4:1,
∴AM:MG=3:1,
∴S△ADM:S△DMG=3:1,
∴S△AMD=3S△DMG ,
∴△AMD,△DMG和△BEG的面积之比为:3:1:4.
所以答案是:3:1:4.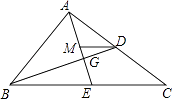
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:
①CF=AE;②OE=OF;③图中共有四对全等三角形;④四边形ABCD是平行四边形;其中正确结论的是_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地电话拨号上网有两种收费方式,用户可以任选其一:(A)计时制,0.05元∕分;(B)包月制,50元∕分(限一部个人住宅电话上网);此外,每种上网方式都附加通信费0.02元∕分。
(1)某用户某月上网时间为x分钟,则该用户在A、B两种收费方式下应支付费用各多少元?
(2)如果一个月内上网200分钟和300分钟,按两种收费方式各需交费多少元?
(3)是否存在某一时间,会出现两种收费方式一样的情况吗?求出这时的上网时间?
(4)如果某人一个月上网20小时,那么应选用哪一种方式较为合算?如果小明的妈妈准备办理这种业务,你能告诉她如何选择更加合算吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12
【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂去年的总产值比总支出多500万元.由于今年总产值比去年增加15%,总支出比去年节约10%,因此,今年总产值比支出多950万元.今年的总产值和总支出各是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两个村庄的坐标分别为(2,2)、(7,4),一辆汽车从原点O出发,在x轴上行驶.
(1)汽车行驶到什么位置时离村庄A最近?写出此位置的坐标.
(2)汽车行驶到什么位置时离村庄B最近?写出此位置的坐标.
(3)请在图中画出汽车到两村庄的距离和最短的位置,并求出此最短的距离和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=里. 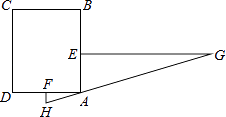
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com