
 Ϊ����ѧ���˽��֪ʶ����ǿ������ʶ��ij��ѧ������һ�λ���֪ʶ����������900��ѧ���μ�����ξ�����Ϊ�˽Ȿ�ξ����ɼ���������г�ȡ�˲���ѧ���ijɼ�����ͳ�ƣ����������δ��ɲ��оֲ������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ������������⣺
Ϊ����ѧ���˽��֪ʶ����ǿ������ʶ��ij��ѧ������һ�λ���֪ʶ����������900��ѧ���μ�����ξ�����Ϊ�˽Ȿ�ξ����ɼ���������г�ȡ�˲���ѧ���ijɼ�����ͳ�ƣ����������δ��ɲ��оֲ������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ������������⣺| ���� | Ƶ�� |
| 50.5��60.5 | 4 |
| 60.5��70.5 | 8 |
| 70.5��80.5 | 10 |
| 80.5��90.5 | 16 |
| 90.5��100.5 | 12 |
| �ϼ� | 50 |
���� ��1���ȸ��ݵ�һ���Ƶ�����ȡ��ѧ�����������һ��Ƶ�ʣ�ͬ������ڶ������������Ƶ�ʣ���50��ȥǰ������������ɵõ��������Ƶ��������Ƶ�ʵĺ͵���1��������������Ƶ�ʣ�
��2������Ƶ�ʷֲ�����ȫֱ��ͼ��
��3������Ƶ�ʵ����壬ѡ��Ƶ������һ�飻
��4�������������������ʣ����м��㼴�ɵý⣮
��� 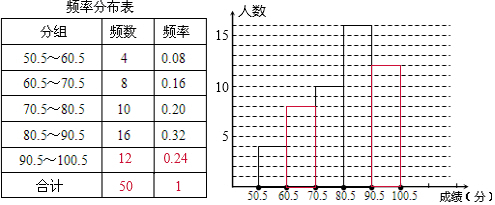 �⣺��1������ͼ����Ϣ����һ���Ƶ��Ϊ4����ȡ��ѧ����Ϊ50�����һ��Ƶ��Ϊ4��50=0.08��
�⣺��1������ͼ����Ϣ����һ���Ƶ��Ϊ4����ȡ��ѧ����Ϊ50�����һ��Ƶ��Ϊ4��50=0.08��
�ڶ����Ƶ����8��50=0.16���������Ƶ����10��50=0.20���������Ƶ����16��50=0.32��
�������Ƶ����50-4-8-10-16=50-38=12���������Ƶ����1-0.08-0.16-0.20-0.32=1-0.76=0.24��
Ƶ�ʷֲ�����ͼ��
�ʴ�Ϊ12��
��2��Ƶ��ֱ��ͼ��ͼ��
��3��ȫ�����ѧ���У������ɼ�����80.5��90.5��һ�鷶Χ�ڵ�������࣮
�ʴ�Ϊ80.5��90.5��
��4��900��0.24=216��
���� ���⿼���Ƶ���ֲ�ֱ��ͼ������������ͳ��ͼ��ȡ��Ϣ������������ͳ��ͼ��ȡ��Ϣʱ����������۲졢�������о�ͳ��ͼ������������ȷ���жϺͽ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -8��1 | B�� | 8 | C�� | -8��2 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ĸ���������-1 | |
| B�� | �κ��������ľ���ֵ�������� | |
| C�� | 0�������� | |
| D�� | �����������Ϊ�෴������ô���ǵľ���ֵ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
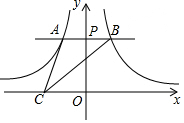 ��ͼ����y��������һ��P����x���ƽ���ߣ��ֱ��뷴��������$y=-\frac{3}{x}$��$y=\frac{1}{x}$��ͼ����A���B�㣬����CΪx��������һ�㣬����AC��BC�����ABC�����Ϊ2��
��ͼ����y��������һ��P����x���ƽ���ߣ��ֱ��뷴��������$y=-\frac{3}{x}$��$y=\frac{1}{x}$��ͼ����A���B�㣬����CΪx��������һ�㣬����AC��BC�����ABC�����Ϊ2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��1 | B�� | m��1 | C�� | m��1�� m��0 | D�� | m��1�� m��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
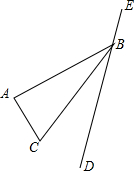 ��ͼ�⣺������ͼ�Σ���д�����ۣ�
��ͼ�⣺������ͼ�Σ���д�����ۣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ھ���ABCD�У�E��AD�ߵ��е㣬BE��AC������Ϊ��F������DF��������������ۣ��١�AEF�ס�CAB����CF=3AF����DF=DC����tan��CAD=$\sqrt{2}$����S��ABF��S�ı���BCDF=1��4�����У���ȷ���Ǣ٢ۢݣ�����ţ���
��ͼ���ھ���ABCD�У�E��AD�ߵ��е㣬BE��AC������Ϊ��F������DF��������������ۣ��١�AEF�ס�CAB����CF=3AF����DF=DC����tan��CAD=$\sqrt{2}$����S��ABF��S�ı���BCDF=1��4�����У���ȷ���Ǣ٢ۢݣ�����ţ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com