
【题目】如图1,点A是线段BC上一点,△ABD和△ACE都是等边三角形.
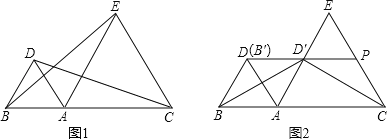
(1)连结BE,CD,求证:BE=CD;
(2)如图2,将△ABD绕点A顺时针旋转得到△AB′D′.
①当旋转角为 度时,边AD′落在AE上;
②在①的条件下,延长DD’交CE于点P,连接BD′,CD′.当线段AB、AC满足什么数量关系时,△BDD′与△CPD′全等?并给予证明.
【答案】解:(1)见详解;(2)① 60;②当AC=2AB时,△BDD′与△CPD′全等.理由见详解.
【解析】
(1)根据等边三角形的性质可得AB=AD,AE=AC,∠BAD=∠CAE=60°,然后求出∠BAE=∠DAC,再利用“边角边”证明△BAE和△DAC全等,根据全等三角形对应边相等即可得证;
(2)①求出∠DAE,即可得到旋转角度数;
②当AC=2AB时,△BDD′与△CPD′全等.根据旋转的性质可得AB=BD=DD′=AD′,然后得到四边形ABDD′是菱形,根据菱形的对角线平分一组对角可得∠ABD′=∠DBD′=30°,菱形的对边平行可得DP∥BC,根据等边三角形的性质求出AC=AE,∠ACE=60°,然后根据等腰三角形三线合一的性质求出∠PCD′=∠ACD′=30°,从而得到∠ABD′=∠DBD′=∠BD′D=∠ACD′=∠PD′C=30°,然后利用“角边角”证明△BDD′与△CPD′全等.
(1)证明:∵△ABD和△ACE都是等边三角形
∴AB=AD,AE=AC,∠BAD=∠CAE=60°,
∴∠BAD+∠DAE=∠CAE+∠DAE,
即∠BAE=∠DAC,
在△BAE和△DAC中,
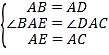 ,
,
∴△BAE≌△DAC(SAS),
∴BE=CD;
(2)①∵∠BAD=∠CAE=60°,
∴∠DAE=180°60°×2=60°,
∵边AD′落在AE上,
∴旋转角=∠DAE=60°.
故答案为:60.
②当AC=2AB时,△BDD′与△CPD′全等.
理由如下:由旋转可知,AB′与AD重合,
∴AB=BD=DD′=AD′,
∴四边形ABDD′是菱形,
∴∠ABD′=∠DBD′=![]() ∠ABD=12×60°=30°,DP∥BC,
∠ABD=12×60°=30°,DP∥BC,
∵△ACE是等边三角形,
∴AC=AE,∠ACE=60°,
∵AC=2AB,
∴AE=2AD′,
∴∠PCD′=∠ACD′=![]() ∠ACE=
∠ACE=![]() ×60°=30°,
×60°=30°,
又∵DP∥BC,
∴∠ABD′=∠DBD′=∠BD′D=∠ACD′=∠PCD′=∠PD′C=30°,
在△BDD′与△CPD′中,
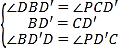 ,
,
∴△BDD′≌△CPD′(ASA).


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①ac>0;②b2>4ac;③4a+2b+c>0;④3a+c>0.其中正确的有( )
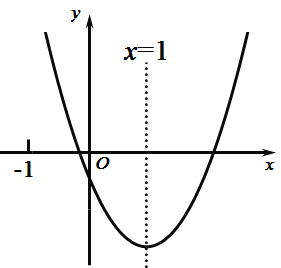
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
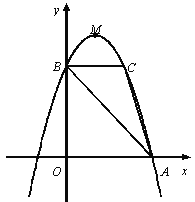
【题目】如图,抛物线y=ax 2+bx+c的顶点为M(1,4),与x轴的右交点为A,与y轴的交点为B,点C与点B关于抛物线的对称轴对称,且S△ABC =3.
(1)求抛物线的解析式;
(2)点D是y轴上一点,将点D绕C点逆时针旋转90°得到点E,若点E恰好落在抛物线上,请直接写出点D的坐标;
(3)设抛物线的对称轴与直线AB交于点F,问:在x轴上是否存在点P,使得以P、A、F为顶点的三角形与△ABC相似?若存在,求点P的坐标;若不存在,请说明理由


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣![]() ,
,![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
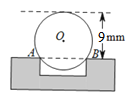
【题目】工程上常用钢珠来测量零件上小孔的直径.假设钢珠的直径是12毫米,测得钢珠顶端离零件表面的距离为9毫米,如图所示,则这个小孔的直径AB是_________毫米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】好山好水好江山,石拱桥在江山处处可见,小明要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥,现测得桥下水面宽度16m时,拱顶高出水平 面4m,货船宽12m,船舱顶部为矩形并高出水面3m。
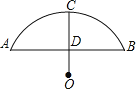
(1)请你帮助小明求此圆弧形拱桥的半径;
(2)小明在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=8,BC=6,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转99次后顶点A在整个旋转过程中所经过的路程之和是( )
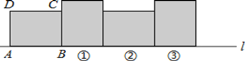
A.288πB.294πC.300πD.396π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3![]() ,求弦AD的长.
,求弦AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com