
����Ŀ����ɽ��ˮ�ý�ɽ��ʯ�����ڽ�ɽ�����ɼ���С��Ҫ��æ�������һ�һ����Ƿ��ܹ���ȫͨ��һ��Բ���εĹ��ţ��ֲ������ˮ�����16mʱ�������߳�ˮƽ ��4m��������12m�����ն���Ϊ���β��߳�ˮ��3m��
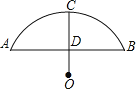
��1���������С�����Բ���ι��ŵİ뾶��
��2��С���ڽ���������ʱ�������ѣ������ж�һ�£��˻�����˳��ͨ������������˵˵�������.
���𰸡���1����Բ���ι��ŵİ뾶Ϊ10m����2���˻�����˳������ͨ����������.���ɼ�����.
��������
��1������OA�����ô����������ɶ������췽�̣�������ŵİ뾶����
��2����ͼ��EF��Ϊ12��ʱ��ͨ�������ˮ��߶�DG�ij������������3�����Ƚ����ж������ܷ�ͨ�����ȸ��ݰ���FG���뾶�����ľ�OG����ֱ�����������OG�ij����жϣ�
��1���⣺����OA��

�������֪CD=4��AB=16��OC��AB�ڵ�D��
��![]() ,
,
��OA=r����OD=r-4
�ࣨr-4��2+82=r2 ��
��֮��r=10
�𣺴�Բ���ι��ŵİ뾶Ϊ10m.
��2���⣺��ͼ

��EF=12
��FG=12��2=6
��OG=![]()
��OD=10-4=6
��DG=OG-OD=8-6=2��3
��˻�����˳������ͨ����������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
��![]() ��������
��������![]() ��
��![]() ����
����![]() �����������
�����������![]() ��
��![]() ��������������.
��������������.
��1����֪![]() ��
��![]() ���������������ߣ�
���������������ߣ�
��![]() ��ֵΪ______��
��ֵΪ______��
������ͼ������ϵ�л������ǵĴ���ͼ��ֱ��д�����ǵĽ�������.
��2����������![]() ��
��![]() ��
��![]()
![]() �Ķ���ֱ�Ϊ
�Ķ���ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��
���ж������Ƿ����������������ߣ���______����������������������
����![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
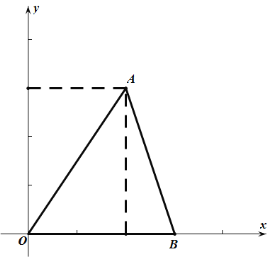
����Ŀ����ͼ��ƽ��ֱ������ϵxOy��,��A��2��3��,B��3��0��,C��m��n������m>0������O��A��B��CΪ������ı�����ƽ���ı��Σ����C������Ϊ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����A���߶�BC��һ�㣬��ABD����ACE���ǵȱ������Σ�
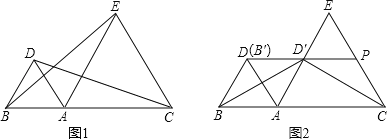
��1������BE��CD����֤��BE=CD��
��2����ͼ2������ABD�Ƶ�A˳ʱ����ת�õ���AB��D����
������ת��Ϊ�� ����ʱ����AD������AE�ϣ�
�������������£��ӳ�DD����CE�ڵ�P������BD����CD�������߶�AB��AC����ʲô������ϵʱ����BDD������CPD��ȫ�ȣ�������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��4��ͬ�ͺŵIJ�Ʒ�У���1�����ϸ�Ʒ��3���ϸ�Ʒ.
��1������4����Ʒ�������ȡ1�����м�⣬ֱ��д���鵽���Dz��ϸ�Ʒ�ĸ��ʣ�
��2������4����Ʒ�������ȡ2�����м�⣬�����б�������״ͼ������鵽�Ķ��Ǻϸ�Ʒ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪ʶ���飺
��1��һ�κ�������ʽ ����k>0��b>0ʱ��ͼ�� ���ޣ���k>0��b<0ʱ��ͼ�� ���ޣ���k<0��b>0ʱ��ͼ�� ���ޣ���k<0��b<0ʱ��ͼ�� ���ޣ��ر�b=0ʱ��ͼ�� ����Ϊ ������
��2���������������ֱ��﷽ʽ�ֱ�Ϊ�� �� �� ������������ͼ���Ϊ ����k>0ʱ��ͼ���� �� ���ޣ�y��x������� ����k<0ʱ��ͼ���� �� ���ޣ�y��x������� ��
��3���������Ǻ���ֵ��
0�� | 30�� | 45�� | 60�� | 90�� | |
sinA | |||||
cosA | |||||
tanA | |||||
cotA |
��4�����κ�������ʽ��
��һ��ʽ�� ��
�ڶ���ʽ�� �� �� ��
��
������ʽ����ʽ���� ��
���Գ��ṫʽ�� �������깫ʽ�� ��
�����κ���ͼ���Ϊ ����a>0ʱ��ͼ���� ����a<0ʱ��ͼ���� ��c>0ʱ��ͼ��� ���������ཻ��c<0ʱ��ͼ��� �Ḻ�����ཻ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��������CEFG�߳��ֱ�Ϊa��b��������CEFG�Ƶ�C��ת���������н��ۣ���BE��DG����BE��DG����DE2+BG2��2a2+b2��������ȷ������_____(�����)
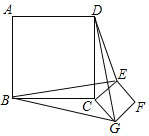
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B�ڷ���������![]() ��k��0����ͼ���ϣ�AC��x�ᣬBD��x�ᣬ����C��D�ֱ���x��������������ϣ�CD=k����֪AB=2AC��E��AB���е㣬����BCE���������ADE�������2������k��ֵ��______��
��k��0����ͼ���ϣ�AC��x�ᣬBD��x�ᣬ����C��D�ֱ���x��������������ϣ�CD=k����֪AB=2AC��E��AB���е㣬����BCE���������ADE�������2������k��ֵ��______��
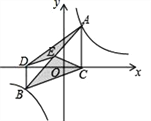
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У���֪��P��m��1��n2����Q��m��n��1��������m��0�������к�����ͼ�����ͬʱ����P��Q������ǣ�������
A.y��2x+bB.y����x2+2x+c
C.y��ax+2 ��a��0��D.y��ax2��2ax+c��a��0��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com