
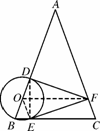
已知:如图N19,在△ABC中,AB=AC=6,cosB=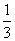 ,⊙O的半径为OB,圆心在AB上,且分别与边AB,BC相交于D,E两点,但⊙O与边AC不相交,又EF⊥AC,垂足为F.
,⊙O的半径为OB,圆心在AB上,且分别与边AB,BC相交于D,E两点,但⊙O与边AC不相交,又EF⊥AC,垂足为F.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)设OB=x,CF=y.
①求y关于x的函数关系式;
②当直线DF与⊙O相切时,求OB的长.
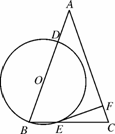
图N19
解:(1)直线EF与⊙O相切.理由如下:
如图104(1),连接OE,
则OE=OB,∠OBE=∠OEB.
∵AB=AC,∴∠OBE=∠C,∴∠OEB=∠C.
∴OE∥AC.∵EF⊥AC,∴EF⊥OE.
∵点E在⊙O上,∴直线EF与⊙O相切.
(2)①如图104(1),作AH⊥BC,H为垂足,
那么BH=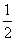 BC.
BC.
∵AB=6,cosB=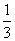 ,∴BH=2,BC=4.
,∴BH=2,BC=4.
∵OE∥AC,∴△BOE∽△BAC.
∴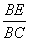 =
=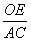 ,即
,即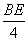 =
=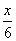 ,
,
∴BE=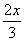 .∴EC=4-
.∴EC=4-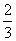 x.
x.
在Rt△ECF中,cosC=cos B=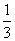 ,
,
∴CF=EC·cosC=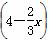 ×
×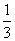 ,
,
∴所求函数的关系式为y=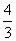 -
-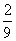 x.
x.
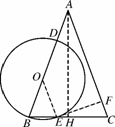
(1) (2)
图104
②如图104(2),连接OE,DE,OF,
由EF,DF与⊙O相切,
∴FD=FE,且∠DFO=∠EFO,
则OF垂直平分DE.
由∠DEB=90°,∴BC⊥DE.
∴OF∥BC,则四边形OBCF是等腰梯形.
∴OB=CF,得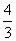 -
-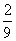 x=x,
x=x,
解得x=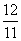 ,即OB=
,即OB=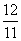 .
.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
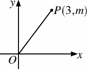
如图6512,在直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OP与x轴正半轴的夹角α的正切值是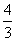 ,则sinα的值为( )
,则sinα的值为( )
A.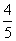 B.
B. 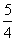 C.
C. 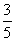 D.
D.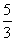
查看答案和解析>>
科目:初中数学 来源: 题型:
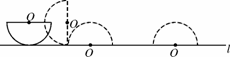
已知一个直径为2米的半圆形工件,未搬动前如图N16,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面向右平移10米,则圆心O所经过的路线长是________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
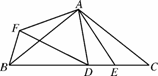
如图N23,在△ABC 中,AB=AC,∠BAC=120°,D,E是BC上的两点,且∠DAE=30°,将△AEC绕点A顺时针旋转120°后,得到△AFB,连接DF.下列结论中正确的个数有( )
①∠FBD=60°;②△ABE∽△DCA;③AE平分∠CAD;④△AFD是等腰直角三角形.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
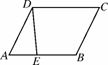
如图N29,已知E是平行四边形ABCD的边AB上的点,连接DE.
(1)在∠ABC的内部,作射线BM交线段CD于点F,使∠CBF=∠ADE(要求:用尺规作图,保留作图痕迹,不写作法和证明);
(2)在(1)的条件下,求证:△ADE≌△CBF.
查看答案和解析>>
科目:初中数学 来源: 题型:
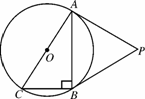
已知:如图N38,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=2 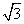 ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com