
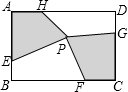
 如图,在矩形SBCD中,点E、F、H分别在边AB、BC、CD、DA上,点P在矩形ABCD内,若AB=6,BC=8,AE=CG=4,BF=DH=6,四边形AEPH的面积为11,则四边形PFCG的面积为11.
如图,在矩形SBCD中,点E、F、H分别在边AB、BC、CD、DA上,点P在矩形ABCD内,若AB=6,BC=8,AE=CG=4,BF=DH=6,四边形AEPH的面积为11,则四边形PFCG的面积为11. 分析 连接AP、CP.把该四边形分解为三角形进行解答.设△AHP在AH边上的高为x,△AEP在AE边上的高为y.得出AH=CF,AE=CG.然后得出S四边形AEPH=S△AHP+S△AEP.根据题意可求解.
解答 解:连接AP,CP,如图所示:
设△AHP在AH边上的高为x,△AEP在AE边上的高为y.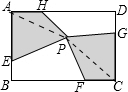
则△CFP在CF边上的高为6-x,△CGP在CG边上的高为8-y.
∵AH=CF=8-6=2,AE=CG=4,
∴S四边形AEPH=S△AHP+S△AEP.
=AH×x×+AE×y×$\frac{1}{2}$,
=2x×$\frac{1}{2}$+4y×$\frac{1}{2}$=11,
∴2x+4y=22,
S四边形PFCG=S△CGP+S△CFP=CF×(6-x)×$\frac{1}{2}$+CG×(8-y)×$\frac{1}{2}$,
=2(6-x)×$\frac{1}{2}$+4(8-y)×$\frac{1}{2}$,
=(44-2x-4y)×$\frac{1}{2}$=(44-22)×$\frac{1}{2}$=11.
故答案为11.
点评 本题考查了矩形的性质、三角形面积的计算等知识点;把四边形的面积分解为三角形的面积来求解是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 哥哥的身高比弟弟高是必然事件 | |
| B. | 今年中秋节有雨是不确定事件 | |
| C. | 随机抛一枚均匀的硬币两次,都是正面朝上是不可能事件 | |
| D. | “彩票中奖的概率为$\frac{1}{5}$”表示买5张彩票肯定会中奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com