
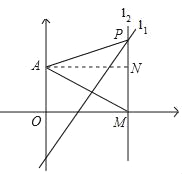
【题目】在平面直角坐标系中,点A(0,2),在x轴上任取一点M,连接AM,作AM的垂直平分线l1.过点M作x轴的垂线l2,l1与l2交于点P.设P点的坐标为(x,y).
(Ⅰ)当M的坐标取(3,0)时,点P的坐标为 ;
(Ⅱ)求x,y满足的关系式;
(Ⅲ)是否存在点M,使得△MPA恰为等边三角形?若存在,求点M的坐标;若不存在,说明理由.
【答案】(Ⅰ)(3,![]() );(Ⅱ)x,y满足的关系式是y=
);(Ⅱ)x,y满足的关系式是y=![]() x2+1;(Ⅲ)△MPA为等边三角形时,点M的坐标为(2
x2+1;(Ⅲ)△MPA为等边三角形时,点M的坐标为(2![]() ,0)或(﹣2
,0)或(﹣2![]() ,0).
,0).
【解析】分析:(Ⅰ)作AN⊥PM于N,根据线段垂直平分线的性质得到PA=PM,根据勾股定理计算;
(Ⅱ)分点M在x轴的正半轴上、点M在x轴的负半轴上两种情况,根据勾股定理列式计算;
(Ⅲ)由(Ⅰ)可知,PA=PM,设点M的坐标为(0,x),根据勾股定理列方程求出x的值.
详解:(Ⅰ)作AN⊥PM于N,
则四边形AOMN是矩形,
∴AN=OM=3,MN=OA=2,
∵l1是AM的垂直平分线,
∴PA=PM,
在Rt△APN中,AN2+PN2=AP2,即32+(y﹣2)2=y2,
解得,y=![]() ,
,
∴点P的坐标为(3,![]() ),
),
故答案为:(3,![]() );
);
(Ⅱ)当点M在x轴的正半轴上时,
在Rt△APN中,AN2+PN2=AP2,即x2+(y﹣2)2=y2,
解得,y=![]() x2+1,
x2+1,
同理,当点M在x轴的负半轴上时,x,y满足的关系式是y=![]() x2+1,
x2+1,
∴x,y满足的关系式是y=![]() x2+1;
x2+1;
(Ⅲ)由(Ⅰ)可知,PA=PM,
要使△MPA为等边三角形,只需MA=MP即可,
∵点A的坐标为(0,2),点M的坐标为(0,x),
∴AM=![]() ,
,
则![]() x2+1=
x2+1=![]() ,
,
解得,x=±2![]() ,
,
∴△MPA为等边三角形时,点M的坐标为(2![]() ,0)或(﹣2
,0)或(﹣2![]() ,0).
,0).


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图①,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() ,将一直角三角板的直角顶点放在点
,将一直角三角板的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的上方.
的上方.
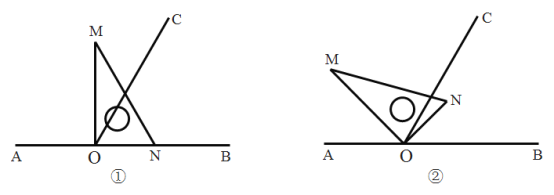
(1)在图①中,![]() __________度;
__________度;
(2)将图①中的三角板绕点![]() 按逆时针方向旋转,使得
按逆时针方向旋转,使得![]() 在
在![]() 的内部,如图②,若
的内部,如图②,若![]() ,求
,求![]() 的度数;
的度数;
(3)将图①中的三角板绕点![]() 以每秒
以每秒![]() 的速度沿逆时针方向旋转一周,在旋转的过程中,当直线
的速度沿逆时针方向旋转一周,在旋转的过程中,当直线![]() 恰好平分锐角
恰好平分锐角![]() 时,旋转的时间是__________秒.(直接写出结果)
时,旋转的时间是__________秒.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
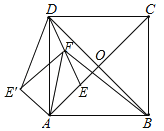
【题目】如图,正方形ABCD中,对角线AC、BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF、BF、E′F.若AE=2![]() .则四边形ABFE′的面积是_____.
.则四边形ABFE′的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某核桃种植基地计划种植A、B两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.
(1)若该基地收获两种核桃的年总产量为25800千克,则A、B两种核桃各种植了多少亩?
(2)设该基地种植A种核桃a亩,全部收购后,总收入为w元,求出w与a之间的函数关系式.若要求种植A种核桃的面积不少于B种核桃的一半,那么种植A、B两种核桃各多少亩时,该种植基地的总收入最多?最多是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鞋号是指鞋子的大小,中国于60年代后期,在全国测量脚长的基础上制定了“中国鞋号”,1998年政府发布了基于![]() 系统,用毫米做单位的中华人民共和国国家标准
系统,用毫米做单位的中华人民共和国国家标准![]() ,被称为“新鞋号”,之前以厘米为单位的鞋号从此被称为“旧鞋号”.新旧鞋号部分对应表如下:
,被称为“新鞋号”,之前以厘米为单位的鞋号从此被称为“旧鞋号”.新旧鞋号部分对应表如下:
新鞋号 | 220 | 225 | 230 | 235 | … | 270 |
旧鞋号 | 34 | 35 | 36 | 37 | … |
|
(1)![]() 的值为______;
的值为______;
(2)若新鞋号为![]() ,旧鞋号为
,旧鞋号为![]() ,则把旧鞋号转换为新鞋号的公式为______
,则把旧鞋号转换为新鞋号的公式为______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数学活动课中,小敏为了测量校园内旗杆![]() 的高度.先在教学楼的底端
的高度.先在教学楼的底端![]() 点处,观测到旗杆顶端
点处,观测到旗杆顶端![]() 得
得![]() ,然后爬到教学楼上的
,然后爬到教学楼上的![]() 处,观测到旗杆底端
处,观测到旗杆底端![]() 的俯角是
的俯角是![]() .已知教学楼中
.已知教学楼中![]() 、
、![]() 两处高度为
两处高度为![]() 米.
米.
(1)求教学楼与旗杆的水平距离![]() ;(结果保留根号);
;(结果保留根号);
(2)求旗杆![]() 的高度.
的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数 1 至 2024 按一定规律排列成如图所示的 8 列,规定从上到下依次为第 1 行,第 2 行,第 3 行,…从左往右依次为第 1 列至第 8 列.
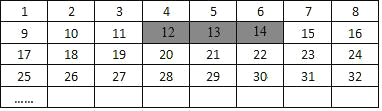
(1)数 56 在第 行 列 ;
(2)平移图中带阴影的方框,使方框框住相邻的三个数,若被框住的三个数中最大的一个数为 x,则被框的三个数的和能否等于 2019?若能,请求出 x;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年九江正在创建“全国文明城市”,小华就公众对在餐厅吸烟的态度进行了随机抽样调查,主要有四种态度:A. 顾客出面制止;B. 劝说进吸烟室;C. 餐厅老板出面制止;D. 无所谓.他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:

(1)这次抽样的公众有______人;
(2)请将统计图①补充完整;
(3)在统计图②中,求出“无所谓”部分所对应的圆心角的度数;
(4)若城区人口有20万人,估计赞成“餐厅老板出面制止”的有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_____.
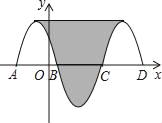
【答案】32
【解析】试题分析:∵抛物线y=﹣x2﹣2x+3与x轴交于点A、B,
∴当y=0时,则﹣x2﹣2x+3=0,
解得x=﹣3或x=1,
则A,B的坐标分别为(﹣3,0),(1,0),
AB的长度为4,
从C1,C3两个部分顶点分别向下作垂线交x轴于E、F两点.
根据中心对称的性质,x轴下方部分可以沿对称轴平均分成两部分补到C1与C2.
如图所示,阴影部分转化为矩形.
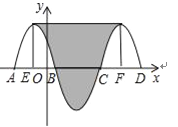
根据对称性,可得BE=CF=4÷2=2,则EF=8
利用配方法可得y=﹣x2﹣2x﹣3=﹣(x+1)2+4
则顶点坐标为(﹣1,4),即阴影部分的高为4,
S阴=8×4=32.
考点:抛物线与x轴的交点.
【题型】填空题
【结束】
17
【题目】解方程:(1)2(3x﹣1)=16;(2)![]() ;(3)
;(3)![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com