
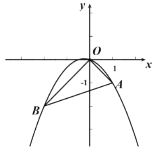
【题目】如图,二次函数![]() 的图像经过
的图像经过![]() 的三个顶点,其中
的三个顶点,其中![]() ,
,![]()
(1)求点![]() 的坐标;
的坐标;
(2)在第三象限存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形,求满足条件的点
为顶点的四边形是平行四边形,求满足条件的点![]() 的坐标;
的坐标;
(3)在(2)的条件下,能否将抛物线![]() 平移后经过
平移后经过![]() 两点,若能求出平移后经过
两点,若能求出平移后经过![]() 两点的拋物线的表达式,并写出平移过程.若不能,请说明理由.
两点的拋物线的表达式,并写出平移过程.若不能,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)能,
;(3)能,![]() ,原抛物线向左平移
,原抛物线向左平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位得到,
个单位得到,![]() 原抛物线先向右平移1个单位,再向下平移1个单位得到
原抛物线先向右平移1个单位,再向下平移1个单位得到
【解析】
(1)把A(1,m)代入函数式而解得m的值,同理解得n值,从而得到A,B的坐标;
(2)①分别过![]() 的三个顶点作对边的平行线,三条平行线两两相交于点
的三个顶点作对边的平行线,三条平行线两两相交于点![]() ,根据平行四边形的性质可求出点C的坐标;
,根据平行四边形的性质可求出点C的坐标;
②分别考虑函数图象经过A,C1,和A,C2时,求出抛物线表达式,再求出平移方式.
解:(1)![]() 的图象过点
的图象过点![]() ,
,
![]() ,
,
同理:![]() ,
,
![]() ,
,![]() ;
;
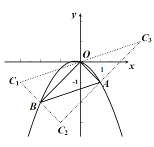
(2)分别过![]() 的三个顶点作对边的平行线,三条平行线两两相交于点
的三个顶点作对边的平行线,三条平行线两两相交于点![]() .
.
因此,四边形![]() ,四边形
,四边形![]() ,四边形
,四边形![]() 为平行四边形.
为平行四边形.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
因此,满足条件的点![]() 坐标为
坐标为![]() ,
,![]() ;
;
(3)能.
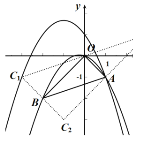
①当平移后的抛物线经过A,C1两点时,
![]() ,
,![]() ,
,
设经过![]() ,
,![]() 两点的抛物线的表达式为
两点的抛物线的表达式为![]() ,
,
依题意,得![]() ,解得
,解得![]() ,
,
![]() 经过
经过![]() 两点的抛物线的表达式为
两点的抛物线的表达式为![]() ,
,
![]() 该抛物线的顶点坐标为
该抛物线的顶点坐标为![]() ,而原抛物线顶点坐标为
,而原抛物线顶点坐标为![]() ,
,
∵![]() ,
, ![]() ,
,
![]() 将原抛物线先向左平移
将原抛物线先向左平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位即可获得符合条件的抛物线;
个单位即可获得符合条件的抛物线;
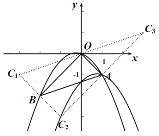
②当平移后的抛物线经过A,C2两点时,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 将
将![]() 点向右平移1个单位再向下平移1个单位使点
点向右平移1个单位再向下平移1个单位使点![]() 移到
移到![]() 点,这时点
点,这时点![]() 随着原抛物线平移到
随着原抛物线平移到![]() 点,
点,
![]() 经过
经过![]() 两点的抛物线的表达式为
两点的抛物线的表达式为![]() ,
,
即![]() ,
,
![]() 将原抛物线先向右平移1个单位,再向下平移1个单位即可获得符合条件的抛物线.
将原抛物线先向右平移1个单位,再向下平移1个单位即可获得符合条件的抛物线.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
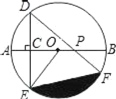
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=2![]() ,∠DPA=45°.则图中阴影部分的面积为____.
,∠DPA=45°.则图中阴影部分的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
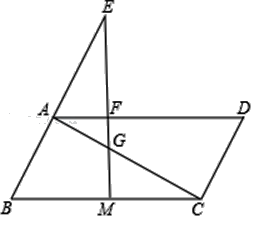
【题目】已知,如图,在平行四边形ABCD中,M是BC边的中点,E是边BA延长线上的一点,连结EM,分别交线段AD、AC于点F、G.
(1)求证:![]() ;
;
(2)当BC2=2BABE时,求证:∠EMB=∠ACD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=ax+b的图象与反比例函数y2=![]() 的图象相交于A、B两点,坐标分别为(—2,4)、(4,—2).
的图象相交于A、B两点,坐标分别为(—2,4)、(4,—2).
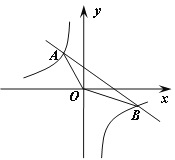
(1)求两个函数的解析式;
(2)求△AOB的面积;
(3)直线AB上是否存在一点P(A除外),使△ABO与以B﹑P、O为顶点的三角形相似?若存在,直接写出顶点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于任意两点
中,对于任意两点![]() ,
,![]() ,如果
,如果![]() ,则称
,则称![]() 与
与![]() 互为“
互为“![]() 距点”.例如:点
距点”.例如:点![]() ,点
,点![]() ,由
,由![]() ,可得点
,可得点![]() 与
与![]() 互为“
互为“![]() 距点”.
距点”.
(1)在点![]() ,
,![]() ,
,![]() 中,原点
中,原点![]() 的“
的“![]() 距点”是_____(填字母);
距点”是_____(填字母);
(2)已知点![]() ,点
,点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() .
.
①当![]() 时,直线
时,直线![]() 上点
上点![]() 的“
的“![]() 距点”的坐标为_____;
距点”的坐标为_____;
②若直线![]() 上存在点
上存在点![]() 的“
的“![]() 点”,求
点”,求![]() 的取值范围.
的取值范围.
(3)已知点![]() ,
,![]() ,
,![]() ,
,![]() 的半径为
的半径为![]() ,若在线段
,若在线段![]() 上存在点
上存在点![]() ,在
,在![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 与点
与点![]() 互为“
互为“![]() 距点”,直接写出
距点”,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面四个实验中,实验结果概率最小的是( )

A.如(1)图,在一次实验中,老师共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,估计出的钉尖朝上的概率
B.如(2)图,是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,指针落在蓝色区域的概率
C.如(3)图,有一个小球在的地板上自由滚动,地板上的每个格都是边长为1的正方形,则小球在地板上最终停留在黑色区域的概率
D.有7张卡片,分别标有数字1,2,3,4,6,8,9,将它们背面朝上洗匀后,从中随机抽出一张,抽出标有数字“大于6”的卡片的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com