练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

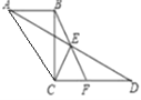
    【题目】如图，AB∥CD，连接AD，点E是AD的中点，连接BE并延长交CD于F点．

    (1)请说明△ABE≌△DFE的理由；

    (2)连接CB，AC，若CB⊥CD，AC=CD，∠D=30°，CD=2，求BF的长．

    【答案】（1）证明见解析；（2）BF=2

    【解析】

    利用三角形全等判定条件ASA进行判断.

    利用30°所对直角边等于斜边的一半求出CE的长，再利用BF=2CE求出BF的长度.

    证明：∵AB∥CD

    ∴∠BAE=∠EDF

    ∵点E是AD的中点

    ∴AE=ED

    又∵∠AEB=∠FED

    ∴△ABE≌△DFE（ASA）

    （2）∵AC=CD 且E为AD中点 ∴CE⊥AD

    ∵∠D=30°且CD=2 ∴CE=1

    又∵CB⊥CD且BE=EF ∴BF=2CE

    ∴BF=2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AD=3，∠CAB=30°，点P是线段AC上的动点，点Q是线段CD上的动点，则AQ+QP的最小值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

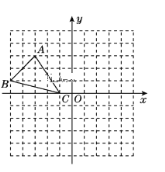
    【题目】如图，已知网格上最小的正方形的边长为1，

    （1）作△ABC关于轴的对称图形△A＇B＇C＇(不写做法）,并写出A＇B＇C＇的坐标，想一想:关于轴对称的两个点之间有什么关系？

    （2）求△ABC的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，已知直线、相交于，，射线从位置起始，绕点逆时针旋转，终边与始边形成的角度为.

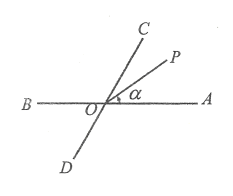
    问题1：若逆时针旋转停止，则

    （1）__________________时，平分；

    （2）__________________时，；

    （3）__________________时，；

    问题2：若逆时针旋转的速度为每秒，在匀速旋转的同时，直线也从图的位置开始绕点逆时针匀速旋转，旋转速度为每秒，当完成旋转一周时，也同时停止旋转.设旋转时间为（）秒.

    （1）旋转时间为多少时，射线与重合.请写出求解过程.

    （2）观察旋转全过程，判断旋转时间为多少时，射线平分.请直接写出的值.（注：指大于且小于的角）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y= x2+bx﹣2与x轴交于A、B两点，与y轴交于C点，且A（一1，0）．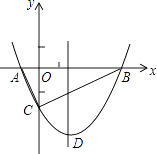

    （1）求抛物线的解析式及顶点D的坐标；
    （2）判断△ABC的形状，证明你的结论；
    （3）点M是抛物线对称轴上的一个动点，当△ACM周长最小时，求点M的坐标及△ACM的最小周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简再求值:当a=9时，求a+的值，甲乙两人的解答如下:

    甲的解答为:原式=a+=a+(1-a)=1.

    乙的解答为:原式=a+=a+(a-1)=2a-1=17.

    两种解答中，_____的解答是错误的,错误的原因是当a=9时______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知某电脑公司有A型、B型、C型三种型号的电脑，其价格分别为A型每台6 000元，B型每台4 000元，C型每台2 500元，我市东坡中学计划将100 500元钱全部用于该电脑公司购进其中两种不同型号的电脑共36台，请你设计出几种不同的购买方案供该校选择，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线EF，CD相交于点0，OA⊥OB，且OC平分∠AOF，

    （1）若∠AOE=40°，求∠BOD的度数；

    （2）若∠AOE=α，求∠BOD的度数；（用含α的代数式表示）

    （3）从（1）（2）的结果中能看出∠AOE和∠BOD有何关系？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，反比例函数y= （x＞0）的图象和矩形ABCD在第一象限，AD平行于x轴，且AB=2，AD=4，点A的坐标为（2，6）．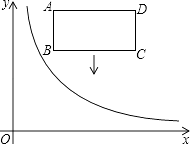

    （1）直接写出B、C、D三点的坐标；
    （2）若将矩形向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，猜想这是哪两个点，并求矩形的平移距离和反比例函数的解析式．

    查看答案和解析>>

    同步练习册答案