
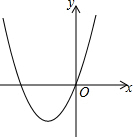
 已知抛物线的顶点为(-2,-3),且经过原点,
已知抛物线的顶点为(-2,-3),且经过原点,分析 (1)由抛物线的对称性可知然后利用待定系数法求解即可;
(2)利用抛物线的对称性可求得与x轴的另一个交点坐标为(-4,0);
(3)根据函数图形确定出x的取值范围即可.
解答 解:(1)∵抛物线的顶点为(-2,-3),且经过原点,
∴抛物线经过点(-4,0).
设抛物线的解析式为y=ax(x+4),将x=-2,y=-3代入得:-4a=-3,
解得:a=$\frac{3}{4}$.
∴抛物线的解析式为y=$\frac{3}{4}$x2+3x.
(2)∵抛物线的顶点为(-2,-3),且经过原点,
∴抛物线经过点(-4,0).
∴抛物线与x轴交点的坐标为(-4,0)、(0,0).
(3)由函数图形可知当-4<x<0时,y<0,
∴x的取值范围是-4<x<0.
点评 本题主要考查的是二次函数的图象和性质,掌握二次函数的图象和性质是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
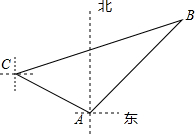 如图,我国海上休渔结束后,甲、乙两艘捕鱼船分别从相距30$\sqrt{2}$千米的A港、C港出海捕鱼,C港在A港北偏西60°处,甲船以每小时15千米的速度沿东北方向航行,甲船航行2小时后乙船快速(匀速)沿北偏东75°的方向航行,结果两船在B处相遇.
如图,我国海上休渔结束后,甲、乙两艘捕鱼船分别从相距30$\sqrt{2}$千米的A港、C港出海捕鱼,C港在A港北偏西60°处,甲船以每小时15千米的速度沿东北方向航行,甲船航行2小时后乙船快速(匀速)沿北偏东75°的方向航行,结果两船在B处相遇.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
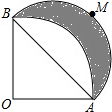 如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2.
如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
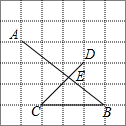 如图,网格图中每个方格都是边长为1的正方形,点A,B,C,D是格点,若线段AB交CD于点E,则线段AE的长是$\frac{20}{7}$.
如图,网格图中每个方格都是边长为1的正方形,点A,B,C,D是格点,若线段AB交CD于点E,则线段AE的长是$\frac{20}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
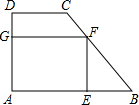 如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=7,CD=4,AD=2,在梯形中作一个矩形AEFG,使E在AB上,F在BC上,G在AD上.
如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=7,CD=4,AD=2,在梯形中作一个矩形AEFG,使E在AB上,F在BC上,G在AD上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com