
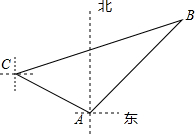
 如图,我国海上休渔结束后,甲、乙两艘捕鱼船分别从相距30$\sqrt{2}$千米的A港、C港出海捕鱼,C港在A港北偏西60°处,甲船以每小时15千米的速度沿东北方向航行,甲船航行2小时后乙船快速(匀速)沿北偏东75°的方向航行,结果两船在B处相遇.
如图,我国海上休渔结束后,甲、乙两艘捕鱼船分别从相距30$\sqrt{2}$千米的A港、C港出海捕鱼,C港在A港北偏西60°处,甲船以每小时15千米的速度沿东北方向航行,甲船航行2小时后乙船快速(匀速)沿北偏东75°的方向航行,结果两船在B处相遇.分析 (1)作AD⊥BC,根据题意求出∠C、∠B的度数,根据锐角三角函数的概念求出AB的长,求出甲船共航行的时间,得到乙船从C处到B处用的时间;
(2)求出BC的长度,根据速度、距离和时间的关系求出答案.
解答 解:(1)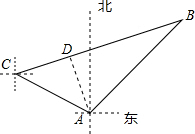 作AD⊥BC,
作AD⊥BC,
由题意得,∠C=45°,由AC=30$\sqrt{2}$,
则AD=CD=30,
∵∠C=45°,∠CAB=105°,
∴∠B=30°,
∴AB=2AD=60,
60÷15=4,
∴甲船共航行了4小时,
则乙船从C处到B处用了2小时;
(2)∵AB=60,AD=30,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=30$\sqrt{3}$,
∴乙船的速度是(30$\sqrt{3}$+30)÷2=15$\sqrt{3}$+15,
答:乙船的速度是每小时15$\sqrt{3}$+15千米.
点评 本题考查的是解直角三角形的应用,正确作出辅助线、掌握锐角三角函数的概念、熟练运用勾股定理是解题的关键.


科目:初中数学 来源: 题型:选择题
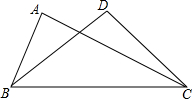 如图,在△ABC和△DCB中,AB=DC,下列四个条件:①AC=DB;②∠A=∠B; ③∠ABC=∠DCB;④∠ACB=∠DBC中,添加其中的一个条件不能使△ABC≌△DCB的有( )
如图,在△ABC和△DCB中,AB=DC,下列四个条件:①AC=DB;②∠A=∠B; ③∠ABC=∠DCB;④∠ACB=∠DBC中,添加其中的一个条件不能使△ABC≌△DCB的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
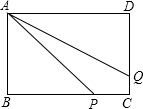 如图,在矩形ABCD中,已知AB=$\sqrt{8}$,BC=$\sqrt{18}$,点P在BC上,点Q在CD上,且CP=2CQ,四边形APCQ的面积是7,求BP的长.
如图,在矩形ABCD中,已知AB=$\sqrt{8}$,BC=$\sqrt{18}$,点P在BC上,点Q在CD上,且CP=2CQ,四边形APCQ的面积是7,求BP的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
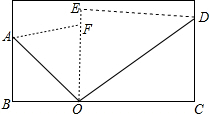 将一张矩形纸片按如图方式折叠,设O点是矩形边上一点,将矩形的一角沿OA翻折使OB与OF重合,再将其邻角沿0D翻折,使OC与OE重合,且O、E、F在同一直线上.求OA与∠BOF、OD与∠EOC的关系.
将一张矩形纸片按如图方式折叠,设O点是矩形边上一点,将矩形的一角沿OA翻折使OB与OF重合,再将其邻角沿0D翻折,使OC与OE重合,且O、E、F在同一直线上.求OA与∠BOF、OD与∠EOC的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
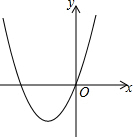 已知抛物线的顶点为(-2,-3),且经过原点,
已知抛物线的顶点为(-2,-3),且经过原点,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-(2x+y-1)=x-2x+y-1 | B. | 3x2-3(x+6)=3x2-3x-6 | ||
| C. | 5a2+(-3a-b)-(2c-d)=5a2-3a-b-2c+d | D. | x-[y-(x+1)]=x-y-z-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
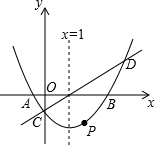 如图,在直角坐标系中,抛物线y=$\frac{1}{3}$x2-mx+n与x轴交于A,B两点,与y轴交于点C,且对称轴是直线x=1.直线y=x-1与抛物线y=$\frac{1}{3}$x2-mx+n相交于C,D两点.点P是抛物线上的动点.
如图,在直角坐标系中,抛物线y=$\frac{1}{3}$x2-mx+n与x轴交于A,B两点,与y轴交于点C,且对称轴是直线x=1.直线y=x-1与抛物线y=$\frac{1}{3}$x2-mx+n相交于C,D两点.点P是抛物线上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com