
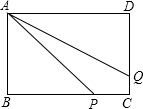
 如图,在矩形ABCD中,已知AB=$\sqrt{8}$,BC=$\sqrt{18}$,点P在BC上,点Q在CD上,且CP=2CQ,四边形APCQ的面积是7,求BP的长.
如图,在矩形ABCD中,已知AB=$\sqrt{8}$,BC=$\sqrt{18}$,点P在BC上,点Q在CD上,且CP=2CQ,四边形APCQ的面积是7,求BP的长. 分析 连接AC,根据四边形APCQ的面积等于△ACQ的面积+△APC的面积=7,可求得CQ的长,从而可求得PC的长,最后根据PB=BC-PC求解即可.
解答 解:连接AC.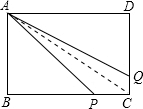
设CQ=x,则PC=2x.
∵四边形APCQ的面积=△ACQ的面积+△APC的面积,
∴$\frac{1}{2}•2x•\sqrt{8}+\frac{1}{2}•x•\sqrt{18}$=7.
解得:x=$\sqrt{2}$.
∴PC=2$\sqrt{2}$.
∴BP=$\sqrt{18}-2\sqrt{2}$=3$\sqrt{2}$-2$\sqrt{2}$=$\sqrt{2}$.
点评 本题主要考查的是三角形的面积公式,根据四边形APCQ的面积=△ACQ的面积+△APC的面积列出关于x的方程是解题的关键.


科目:初中数学 来源: 题型:解答题
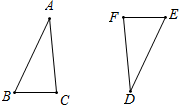 如图,△ABC和△DEF关于点O成心对称.
如图,△ABC和△DEF关于点O成心对称.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 班级 | 平均数 | 方差 | 中位数 | 众数 |
| (1)班 | 168 | 3.2 | 168 | 168 |
| (2)班 | 168 | 3.8 | 168 | 165,167,168,170 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
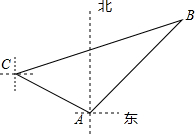 如图,我国海上休渔结束后,甲、乙两艘捕鱼船分别从相距30$\sqrt{2}$千米的A港、C港出海捕鱼,C港在A港北偏西60°处,甲船以每小时15千米的速度沿东北方向航行,甲船航行2小时后乙船快速(匀速)沿北偏东75°的方向航行,结果两船在B处相遇.
如图,我国海上休渔结束后,甲、乙两艘捕鱼船分别从相距30$\sqrt{2}$千米的A港、C港出海捕鱼,C港在A港北偏西60°处,甲船以每小时15千米的速度沿东北方向航行,甲船航行2小时后乙船快速(匀速)沿北偏东75°的方向航行,结果两船在B处相遇.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
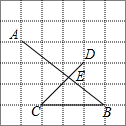 如图,网格图中每个方格都是边长为1的正方形,点A,B,C,D是格点,若线段AB交CD于点E,则线段AE的长是$\frac{20}{7}$.
如图,网格图中每个方格都是边长为1的正方形,点A,B,C,D是格点,若线段AB交CD于点E,则线段AE的长是$\frac{20}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com