
分析 (1)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把已知等式变形后代入计算即可求出值;
(2)由题意得到a,b分别为方程x2+3x+1=0的两根,利用根与系数的关系求出a+b与ab的值,原式变形后代入计算即可求出值.
解答 解:(1)∵a2+2a-1=0,即a2+2a=1,
∴原式=$\frac{{a}^{2}-4-{a}^{2}+a}{a(a+2)^{2}}$•$\frac{a+2}{a-4}$=$\frac{1}{{a}^{2}+2a}$=1;
(2)∵a,b为实数,且a2+3a+1=0,b2+3b+1=0,
∴a,b分别为方程x2+3x+1=0的两根,即a+b=-3,ab=1,
则原式=$\frac{{a}^{2}+{b}^{2}}{ab}$=$\frac{(a+b)^{2}-2ab}{ab}$=7.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
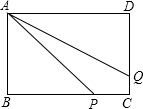 如图,在矩形ABCD中,已知AB=$\sqrt{8}$,BC=$\sqrt{18}$,点P在BC上,点Q在CD上,且CP=2CQ,四边形APCQ的面积是7,求BP的长.
如图,在矩形ABCD中,已知AB=$\sqrt{8}$,BC=$\sqrt{18}$,点P在BC上,点Q在CD上,且CP=2CQ,四边形APCQ的面积是7,求BP的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-(2x+y-1)=x-2x+y-1 | B. | 3x2-3(x+6)=3x2-3x-6 | ||
| C. | 5a2+(-3a-b)-(2c-d)=5a2-3a-b-2c+d | D. | x-[y-(x+1)]=x-y-z-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{6}{5}>-(-\frac{3}{5})$ | B. | -(+3)<-(-4) | C. | 0>-|-3| | D. | +(-2)<-(-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
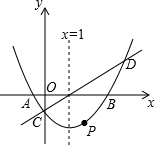 如图,在直角坐标系中,抛物线y=$\frac{1}{3}$x2-mx+n与x轴交于A,B两点,与y轴交于点C,且对称轴是直线x=1.直线y=x-1与抛物线y=$\frac{1}{3}$x2-mx+n相交于C,D两点.点P是抛物线上的动点.
如图,在直角坐标系中,抛物线y=$\frac{1}{3}$x2-mx+n与x轴交于A,B两点,与y轴交于点C,且对称轴是直线x=1.直线y=x-1与抛物线y=$\frac{1}{3}$x2-mx+n相交于C,D两点.点P是抛物线上的动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
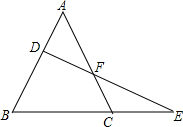 如图,△ABC中,直线DE交AB于D,交AC于F,交BC的延长线于E,求证:$\frac{AD}{DB}$•$\frac{BE}{EC}$•$\frac{CF}{FA}$=1.
如图,△ABC中,直线DE交AB于D,交AC于F,交BC的延长线于E,求证:$\frac{AD}{DB}$•$\frac{BE}{EC}$•$\frac{CF}{FA}$=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com