
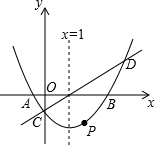 ��ͼ����ֱ������ϵ�У�������y=$\frac{1}{3}$x2-mx+n��x�ύ��A��B���㣬��y�ύ�ڵ�C���ҶԳ�����ֱ��x=1��ֱ��y=x-1��������y=$\frac{1}{3}$x2-mx+n�ཻ��C��D���㣮��P���������ϵĶ��㣮
��ͼ����ֱ������ϵ�У�������y=$\frac{1}{3}$x2-mx+n��x�ύ��A��B���㣬��y�ύ�ڵ�C���ҶԳ�����ֱ��x=1��ֱ��y=x-1��������y=$\frac{1}{3}$x2-mx+n�ཻ��C��D���㣮��P���������ϵĶ��㣮���� ��1�����ݶԳ���x=1�������m��ֵ������ֱ��y=x-1��������y=$\frac{1}{3}$x2-mx+n�ཻ��C��D���㼴�����n��ֵ��������������ߵĽ���ʽ��A��B���������Ҳ�������
��2��������P��ֱ����CDƽ����������������ʱ����CDP��������������������Ľ���ʽ���������������������P�����ꣻ
��3��������������ߵĶ������꣬����ͼ�ηֱ����P����C�㡢���������Լ��ڵ�Bλ��ʱ�ı���APBD����������ͼ�μ����������������S��ȡֵ��
��� �⣺��1����������y=$\frac{1}{3}$x2-mx+n�ĶԳ�����ֱ��x=1��
��m=$\frac{2}{3}$��
��ֱ��y=x-1��������y=$\frac{1}{3}$x2-mx+n�ཻ��C��D���㣬
��C��������0��-1����
��n=-1��
�������߽���ʽΪy=$\frac{1}{3}$x2-$\frac{2}{3}$x-1��
����y=$\frac{1}{3}$x2-$\frac{2}{3}$x-1=0��
��x2-2x-3=0��
��x=-1��x=3��
���A������-1��0������B������3��0����
��2��������P��ֱ����CDƽ����������������ʱ����CDP��������
�����P��ֱ��Ϊy=x+b��
����$\left\{\begin{array}{l}{y=x+b}\\{y=\frac{1}{3}{x}^{2}-\frac{2}{3}x-1}\end{array}\right.$��
��x2-5x-3-3b=0��
��=25-4����-3-3b��=0��
���b=-$\frac{37}{12}$��
����$\left\{\begin{array}{l}{y=x-\frac{37}{12}}\\{y=\frac{1}{3}{x}^{2}-\frac{2}{3}x-1}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=-\frac{7}{12}}\end{array}\right.$��
�ʵ�P������Ϊ��$\frac{5}{2}$��-$\frac{7}{12}$����
��3������$\left\{\begin{array}{l}{y=x-1}\\{y=\frac{1}{3}{x}^{2}-\frac{2}{3}x-1}\end{array}\right.$��
���x=0��x=5��
����D����Ϊ��5��4����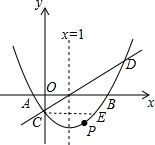 ������y=$\frac{1}{3}$x2-$\frac{2}{3}$x-1�Ķ�������Ϊ��1��-$\frac{4}{3}$��
������y=$\frac{1}{3}$x2-$\frac{2}{3}$x-1�Ķ�������Ϊ��1��-$\frac{4}{3}$��
��C��0��-1������ֱ��x=1�ĶԳƵ�E����Ϊ��2��-1����
��ͼ������Pλ�ڵ�C��ʱ���ı���APBD�����ΪS=S��ACB+S��ABD=$\frac{1}{2}$��4��1+$\frac{1}{2}$��4��4=10��
����Pλ�ڶ������괦ʱ���ı���APBD�����ΪS=S��APB+S��ABD=$\frac{1}{2}$��4��$\frac{4}{3}$+$\frac{1}{2}$��4��4=$\frac{32}{3}$��
����Pλ�ڵ�B��ʱ���ı���APBD�����ΪS=S��ABD=$\frac{1}{2}$��4��4=8��
���Ͽ�֪����8��S��10ʱ��S=$\frac{32}{3}$ʱ�����������ĵ�Pֻ��һ������10��S��$\frac{32}{3}$ʱ�����������ĵ�P��������
���� ������Ҫ�����˶��κ������ۺ��⣬�����漰������ϵ��������κ����Ľ���ʽ�����κ��������ʣ�ƽ���ߵ������Լ��ı��ε������֪ʶ�����2���ʵĹؼ����е�֪ʶ��𣬽��3������Ҫ�������ۣ�������һ�����Ѷȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
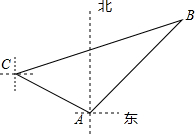 ��ͼ���ҹ�������������ס������Ҳ��㴬�ֱ�����30$\sqrt{2}$ǧ��A�ۡ�C�۳������㣬C����A�۱�ƫ��60�㴦���״���ÿСʱ15ǧ���ٶ��ض��������У��״�����2Сʱ���Ҵ����٣����٣��ر�ƫ��75��ķ����У����������B��������
��ͼ���ҹ�������������ס������Ҳ��㴬�ֱ�����30$\sqrt{2}$ǧ��A�ۡ�C�۳������㣬C����A�۱�ƫ��60�㴦���״���ÿСʱ15ǧ���ٶ��ض��������У��״�����2Сʱ���Ҵ����٣����٣��ر�ƫ��75��ķ����У����������B���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
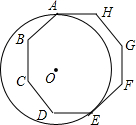 ��ͼ����O�����˱���ABCDEFGH�ı�AH��EF�����ڵ�A��E������O�İ뾶Ϊ4�����ӻ�$\widehat{AE}$�ij�Ϊ3�У�
��ͼ����O�����˱���ABCDEFGH�ı�AH��EF�����ڵ�A��E������O�İ뾶Ϊ4�����ӻ�$\widehat{AE}$�ij�Ϊ3�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
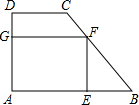 ��ͼ��������ABCD�У�AB��CD����A=90�㣬AB=7��CD=4��AD=2������������һ������AEFG��ʹE��AB�ϣ�F��BC�ϣ�G��AD�ϣ�
��ͼ��������ABCD�У�AB��CD����A=90�㣬AB=7��CD=4��AD=2������������һ������AEFG��ʹE��AB�ϣ�F��BC�ϣ�G��AD�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12.5cm2 | B�� | 25cm2 | C�� | 37.5cm2 | D�� | 50cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
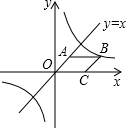 ��ͼ��ʾ����֪����OABC����C��x���ϣ�ֱ��y=x������A������OABC�������$\sqrt{2}$��������������y=$\frac{k}{x}$��ͼ����B����˷�������������ʽ�е�kΪ$\sqrt{2}$+1��
��ͼ��ʾ����֪����OABC����C��x���ϣ�ֱ��y=x������A������OABC�������$\sqrt{2}$��������������y=$\frac{k}{x}$��ͼ����B����˷�������������ʽ�е�kΪ$\sqrt{2}$+1���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com