
分析 先利用加减消元法可解得x=-k+2,y=2k-2,而关于x,y的方程组$\left\{\begin{array}{l}{x+y=k}\\{x-y=4-3k}\end{array}\right.$的解为正数,则x>0且y>0,即$\left\{\begin{array}{l}{-k+2>0}\\{2k-2>0}\end{array}\right.$,然后解不等式组即可得到k的取值范围.
解答 解:方程组$\left\{\begin{array}{l}{x+y=k①}\\{x-y=4-3k②}\end{array}\right.$,
①+②得2x=-2k+4,
∴x=-k+2,
①-②得2y=4k-4,
∴y=2k-2,
∴方程组的解是正数,
可得:$\left\{\begin{array}{l}{-k+2>0}\\{2k-2>0}\end{array}\right.$,
解得:1<k<2.
点评 本题考查了二元一次方程组的解:使二元一次方程组的两个方程左右两边都相等的未知数的值叫二元一次方程组的解.也考查了二元一次方程组的解的情况以及解不等式组.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
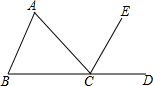 如图,点B、C、D在同一直线上,∠A=∠B.
如图,点B、C、D在同一直线上,∠A=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
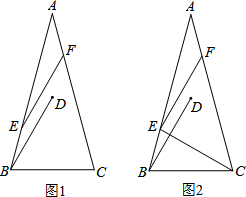 在△ABC 中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.
在△ABC 中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
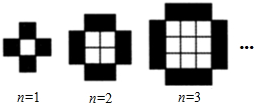 当白色小正方形个数n等于1,2,3,…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n个图形中白色小正方形的个数是n2和黑色小正方形的个数是4n(用n表示,n是正整数).
当白色小正方形个数n等于1,2,3,…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n个图形中白色小正方形的个数是n2和黑色小正方形的个数是4n(用n表示,n是正整数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 图形标号 | (1) | (2) | (3) | (4) |
| 火柴棒根数 | 5 | 9 | 13 | 17 |
| 三角形个数 | 2 | 4 | 6 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
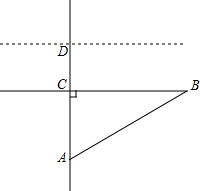 学校池塘的荷叶刚发新芽,如图中虚线所示,测得水深AC为0.6m,荷花根部与荷叶的水平距离CB为0.8m,且AD=AB,忽遇大雨,使池塘水位每小时上升0.1米,问3小时后荷叶是否有没顶之灾?
学校池塘的荷叶刚发新芽,如图中虚线所示,测得水深AC为0.6m,荷花根部与荷叶的水平距离CB为0.8m,且AD=AB,忽遇大雨,使池塘水位每小时上升0.1米,问3小时后荷叶是否有没顶之灾?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com