
【题目】某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系:![]() (t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
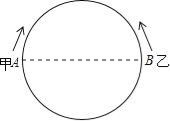
(1)甲运动4s后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
【答案】(1)14cm (2)3s (3)7s
【解析】
试题(1)根据题目所给的函数解析式把t=4s代入求得l的值即可。
(2)根据图可知,二者第一次相遇走过的总路程为半圆,分别求出甲、乙走的路程,列出方程求解即可。
(3)根据图可知,二者第二次相遇走过的总路程为一圈半,也就是三个半圆,分别求出甲、乙走的路程,列出方程求解即可。
解:(1)当t=4s时,![]() =8+6=14(cm),
=8+6=14(cm),
答:甲运动4s后的路程是14cm。
(2)由图可知,甲乙第一次相遇时走过的路程为半圆21cm,
甲走过的路程为![]() ,乙走过的路程为4t,
,乙走过的路程为4t,
则![]() +4t=21,
+4t=21,
解得:t=3或t=﹣14(不合题意,舍去)。
答:甲、乙从开始运动到第一次相遇时,它们运动了3s。
(3)由图可知,甲乙第一次相遇时走过的路程为三个半圆:3×21=63cm,
则![]() +4t=63,
+4t=63,
解得:t=7或t=﹣18(不合题意,舍去)。
答:甲、乙从开始运动到第二次相遇时,它们运动了7s


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,弦BE与弦CD交于点G,点E为 ![]() 的中点,过点B的直线交DC延长线于点A,AB∥DE.
的中点,过点B的直线交DC延长线于点A,AB∥DE.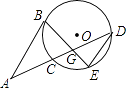
(1)若AB=AG,求证:AB是⊙O切线;
(2)在(1)条件下,若tanA= ![]() ,DE=10,求⊙O的半径.
,DE=10,求⊙O的半径.
(3)求证:AG2﹣BG2=ACAG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC。若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
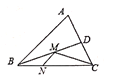
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,D是BC上的一点,且满足∠BAD= ![]() ∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
(1)求证:直线BC是⊙O的切线;
(2)连接EF,若tan∠AEF= ![]() ,AD=4,求BD的长.
,AD=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
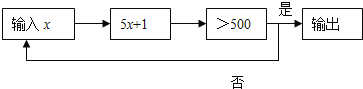
【题目】按下面程序计算,即根据输入的![]() 判断
判断![]() 是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的
是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的![]() 的值作为新的
的值作为新的![]() 的值,继续运算,循环往复,直至输出结果为止.若开始输入
的值,继续运算,循环往复,直至输出结果为止.若开始输入![]() 的值为正整数,最后输出的结果为656,则满足条件的所有
的值为正整数,最后输出的结果为656,则满足条件的所有![]() 的值是__.
的值是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.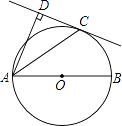
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为5,BC=6,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
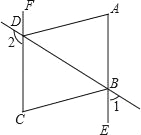
【题目】如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由;
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学知识伴随着人类文明的起源而产生,人类祖先为我们留下了许多珍贵的原始资料,古巴比伦楔形文字泥板书就是其中之一,古巴比伦泥板上记载了两种利用平方数表计算两数乘积的公式:
![]() …①
…①
![]() …②
…②
(1)材料中,公式②中的空缺部分应该是 ;
(2)请你验证材料中的公式①;
(3)当![]() ,
,![]() 时,利用公式①计算
时,利用公式①计算![]() 的值为 .
的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com