
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.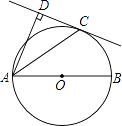
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为5,BC=6,求CD的长.
【答案】
(1)证明:连接OC.如图1所示
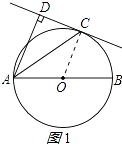
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAC=∠OCA,
∴DA∥OC,
∵AD⊥DC,
∴∠ADC=90°,
∴∠OCD=90°,
即OC⊥DC,
∵OC为半径,
∴DC为⊙O的切线.
(2)解:连接BC,如图2所示:

∵AB是⊙O的直径,
∴AB=10,∠ACB=90°=∠ADC,
∴AC= ![]() =8,
=8,
又∵∠DAC=∠OAC,
∴△ACD∽△ABC,
∴ ![]() ,即
,即 ![]() ,
,
解得:CD=4.8.
【解析】(1)根据切线的判定方法只要求出∠OCD=90°即可;由AC平∠DAB,得到∠DAC=∠OAC,由OA=OC,得到∠OCA=∠OAC,∠DAC=∠OCA,DA∥OC,因为AD⊥DC,所以∠ADC=90°,∠OCD=90°,即OC⊥DC,由OC为半径,所以DC为⊙O的切线;(2)由AB是⊙O的直径,根据勾股定理求出AC的值,又两角相等两三角形相似,得出△ACD∽△ABC,写出比例式求出CD的值.
【考点精析】本题主要考查了切线的判定定理的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下列文字与例题,并解答。
将一个多项式分组进行因式分解后,可用提公因式法或公式法继续分解的方法称作分组分解法。例如:以下式子的分解因式的方法叉称为分组分解法。
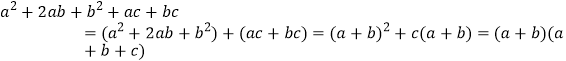 (1)试用“分组分解法”分解因式:
(1)试用“分组分解法”分解因式:![]()
(2)已知四个实数a,b,c,d满足![]() 。并且
。并且![]() ,
,![]() ,
,![]() ,
,![]() 同时成立。
同时成立。
①当k=1时,求a+c的值;
②当k≠0时,用含a的代数式分别表示b、c、d。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系:![]() (t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
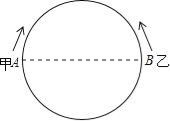
(1)甲运动4s后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:给定两个不等式组![]() 和
和![]() ,若不等式组
,若不等式组![]() 的任意一个解,都是不等式组
的任意一个解,都是不等式组![]() 的一个解,则称不等式组
的一个解,则称不等式组![]() 为不等式组
为不等式组![]() 的“子集”例如:不等式组:
的“子集”例如:不等式组:![]() 是:
是:![]() 的“子集”.
的“子集”.
(1)若不等式组:![]() ,
,![]() ,其中不等式组_________是不等式组
,其中不等式组_________是不等式组![]() 的“子集”(填
的“子集”(填![]() 或
或![]() );
);
(2)若关于![]() 的不等式组
的不等式组![]() 是不等式组
是不等式组![]() 的“子集”,则
的“子集”,则![]() 的取值范围是________;
的取值范围是________;
(3)已知![]() 为互不相等的整数,其中
为互不相等的整数,其中![]() ,
,![]() ,下列三个不等式组:
,下列三个不等式组:![]() ,
,![]() ,
,![]() 满足:
满足:![]() 是
是![]() 的“子集”且
的“子集”且![]() 是
是![]() 的“子集”,则
的“子集”,则![]() 的值为__________;
的值为__________;
(4)已知不等式组![]() 有解,且
有解,且![]() 是不等式组
是不等式组![]() 的“子集”,请写出
的“子集”,请写出![]() ,
,![]() 满足的条件:________________.
满足的条件:________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com