
【题目】某化工材料经销公司购进一种化工原料若干千克,物价部门规定其销售单价不低于进价,不高于60元/千克,经市场调查发现:销售单价定为60元/千克时,每日销售20千克;如调整价格,每降价1元/千克,每日可多销售2千克.
(1)已知某天售出该化工原料40千克,则当天的销售单价为 50 元/千克;
(2)该公司现有员工2名,每天支付员工的工资为每人每天90元,每天应支付其他费用108元,当某天的销售价为46元/千克时,收支恰好平衡. ①求这种化工原料的进价;
②若公司每天的纯利润(收入﹣支出)全部用来偿还一笔10000元的借款,则至少需多少天才能还清借款?
【答案】
(1)解:设某天售出该化工原料40千克时的销售单价为x元/千克,
(60﹣x)×2+20=40,
解得,x=50,
故答案为:50;
(2)解:①设这种化工原料的进价为a元/千克,
当销售价为46元/千克时,当天的销量为:20+(60﹣46)×2=48(千克),
则(46﹣a)×48=108+90×2,
解得,a=40,
即这种化工原料的进价为40元/千克;
②设公司某天的销售单价为x元/千克,每天的收入为y元,
则y=(x﹣40)[20+2(60﹣x)]=﹣2(x﹣55)2+450,
∴当x=55时,公司每天的收入最多,最多收入450元,
设公司需要t天还清借款,
则(450﹣108﹣90×2)t≥10000,
解得,t≥ ![]() ,
,
∵t为整数,
∴t=62.
即公司至少需62天才能还清借款.
【解析】(1)根据销售单价定为60元/千克时,每日销售20千克;如调整价格,每降价1元/千克,每日可多销售2千克,可以求得某天售出该化工原料40千克,当天的销售单价;(2)①根据该公司现有员工2名,每天支付员工的工资为每人每天90元,每天应支付其他费用108元,当某天的销售价为46元/千克时,收支恰好平衡,可以列出相应的方程,从而可以求得原料的进价;②根据题意可以求得每天的最大利润,从而可以求得少需多少天才能还清借款.


科目:初中数学 来源: 题型:
【题目】为加快城市群的建设与发展,在A,B两城市间新建一条城际铁路,建成后,铁路运行里程由现在的120km缩短至114km,城际铁路的设计平均时速要比现行的平均时速快110km,运行时间仅是现行时间的![]() ,求建成后的城际铁路在A,B两地的运行时间.
,求建成后的城际铁路在A,B两地的运行时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
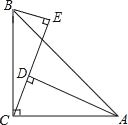
【题目】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.
(1)证明:△BCE≌△CAD;
(2)若AD=25cm,BE=8cm,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①若a<1,则(a﹣1) ![]() =﹣
=﹣ ![]() ;②平行四边形既是中心对称图形又是轴对称图形;③
;②平行四边形既是中心对称图形又是轴对称图形;③ ![]() 的算术平方根是3;④如果方程ax2+2x+1=0有两个不相等的实数根,则实数a<1.其中正确的命题个数是( )
的算术平方根是3;④如果方程ax2+2x+1=0有两个不相等的实数根,则实数a<1.其中正确的命题个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三名射击运动员在某场测试中各射击10次,3人的测试成绩如下表

则甲、乙、丙3名运动员测试成绩最稳定的是 ( )
A.甲 B.乙 C.丙 D.3人成绩稳定情况相同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据提示填空(8分)
如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.

因为EF∥AD
所以∠2=____(____________________________)
又因为∠1=∠2
所以∠1=∠3(______________)
所以AB∥_____(_____________________________)
所以∠BAC+______=180°(_____________________)
因为∠BAC=80° 所以∠AGD=_______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com