
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= ![]() 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
的图象上,OA=1,OC=6,则正方形ADEF的边长为 . 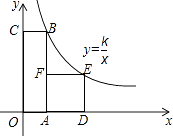
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
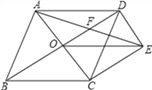
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=![]() AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(﹣2,0),B(0,1).
(1)点C的坐标是;
(2)将△ABC沿x轴正方向平移得到△A′B′C′,且B,C两点的对应点B′,C′恰好落在反比例函数y= ![]() 的图象上,求该反比例函数的解析式.
的图象上,求该反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“化归与转化的思想”是指在研究解决数学问题时采用某种手段将问题通过变换使之转化,进而使问题得到解决:
(1)我们知道m2+n2=0可以得到m=0,n=0.如果a2+b2+2a﹣4b+5=0,求a、b的值.
(2)已知a![]() x+2017,b
x+2017,b![]() x+2015,c
x+2015,c![]() x+2016,试问:多项式a2+b2+c2﹣ab﹣ac﹣bc的值是否与变量x的取值有关?若有关请说明理由;若无关请求出多项式的值.
x+2016,试问:多项式a2+b2+c2﹣ab﹣ac﹣bc的值是否与变量x的取值有关?若有关请说明理由;若无关请求出多项式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(m)与散步所用时间t(min)之间的函数关系,依据图象,下面描述中符合小红散步情景的有_____(填序号)
①从家里出发,到了一个公共阅报栏,看了一会儿报后,继续向前走了一段然后回家了
②小红家距离公共阅报栏300m
③从家出发,一直散步(没有停留),然后回家了
④小红本次散步共用时18min

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数.从中抽取部分同学的成绩进行统计,并绘制成如图统计图.
请根据图中提供的信息,解答下列问题:
(1)所抽取的样本容量为 .
(2)若抽取的学生成绩用扇形图来描述,则表示“第三组(79.5~89.5 )”的扇形的圆心角度数为多少?
(3)如果成绩在80分以上(含80分)的同学可以获奖,请估计该校有多少名同学获奖.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com