
| 年龄(岁) | 12 | 13 | 14 | 15 | 16 |
| 人数 | 1 | 4 | 3 | 5 | 7 |
| A. | 15,14 | B. | 15,15 | C. | 16,14 | D. | 16,15 |
科目:初中数学 来源: 题型:选择题
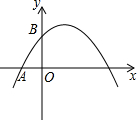 如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )
如图,抛物线y=-x2+ax+4与x轴负半轴交于点A,与y轴交于点B,且tan∠ABO=$\frac{1}{4}$,点C(x1,y1),D(x2,y2)是抛物线y=-x2+ax+4上两点,当x1≤x≤x2,y的取值范围为$\frac{12}{{x}_{2}}$≤y≤$\frac{12}{{x}_{1}}$.则下列结论正确的是( )| A. | a=-3 | B. | y2<4 | C. | |x1-x2|=1 | D. | |x1-$\frac{3}{2}$|>|x2-$\frac{3}{2}$| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙M的圆心M(-1,2),⊙M经过坐标原点O,与y轴交于点A.经过点A的一条直线l解析式为:y=-$\frac{1}{2}$x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(-4,0).
如图,⊙M的圆心M(-1,2),⊙M经过坐标原点O,与y轴交于点A.经过点A的一条直线l解析式为:y=-$\frac{1}{2}$x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(-4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
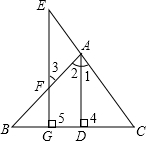 已知:如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.
已知:如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
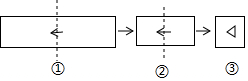 把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )
把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )| A. | 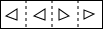 | B. | 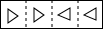 | C. | 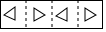 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
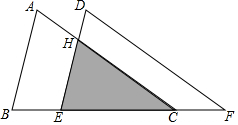 如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=$\sqrt{3}$,则△ABC移动的距离是( )
如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=$\sqrt{3}$,则△ABC移动的距离是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\sqrt{3}$-$\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com