
【题目】如图,等腰三角形ABC中,AB=AC=5cm,BC=6cm,动点P从点A出发,沿路线A﹣B﹣C匀速运动,速度为1cm/s,运动到C点停止,设运动时间为t(s),△APC的面积为y(cm2).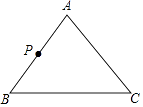
(1)求△ABC的面积.
(2)求等腰△ABC腰上的高.
(3)请分别求出P在边AB(0≤t≤5)、BC(5<t≤11)上运动时,△APC的面积为y(cm2)与运动时间t(s)之间的函数关系式.
(4)是否存在某一时刻t,使得△APC的面积正好是△ABC面积的 ![]() ,若存在,求出t的值;若不存在,说明理由.
,若存在,求出t的值;若不存在,说明理由.
(5)当运动时间t(s)为时,(直接填空)△APC为直角三角形.
【答案】
(1)
解:如图1,
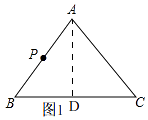
过点A作AD⊥BC,
∵AB=AC=5cm,BC=6cm,
∴BD=CD= ![]() BC=3,
BC=3,
根据勾股定理得,AD= ![]() =4,
=4,
∴S△ABC= ![]() BCAD=
BCAD= ![]() ×6×4=12,
×6×4=12,
即:△ABC的面积为12;
(2)
解:如图2,
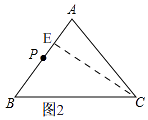
过点C作CE⊥AB,
∵AB=5
∴S△ABC= ![]() ABCE=
ABCE= ![]() ×5CE=
×5CE= ![]() CE
CE
由(1)知,S△ABC=12,
∴ ![]() CE=12,
CE=12,
∴CE= ![]() ,
,
∴等腰△ABC腰上的高为 ![]()
(3)
解:当点P在边AB(0≤t≤5)时,
如图3,
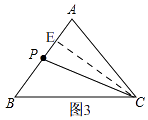
由运动知,AP=t,
∴y=S△APC= ![]() APCE=
APCE= ![]() t×
t× ![]() =
= ![]() t;
t;
当点P在边BC(5<t≤11)时,
如图4,
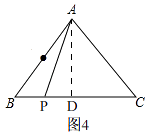
由运动知,PC=5+5﹣t=10﹣t,
∴y=S△APC= ![]() PCAD=
PCAD= ![]() (10﹣t)×4=﹣2t+20
(10﹣t)×4=﹣2t+20
(4)
解:存在,由(1)知,S△ABC=12,
∵△APC的面积正好是△ABC面积的 ![]() ,
,
y= ![]() ×12=5
×12=5
∴当点P在边AB(0≤t≤5)时,y= ![]() t=5,
t=5,
∴t= ![]() ,
,
当点P在边BC(5<t≤11)时,y=﹣2t+20=5,
∴t= ![]() ,
,
即:满足条件的t= ![]() 或
或 ![]()
(5)![]()
或7
【解析】(5)∵AB=AC=5cm,BC=6cm,要使△APC为直角三角形,只有∠APC=90°,
当点P在AB上时,如图2中的点E就是点P,
即:AP=AE,
在Rt△ACE中,AC=5,CE= ![]() ,
,
∴AE= ![]() =
= ![]() ,
,
∴t= ![]() s,
s,
当点P在BC上时,如图1中的点D就是点P,
∴CP=CD=3,
∴(10﹣3)÷1=7s
所以答案是: ![]() 或7.
或7.


科目:初中数学 来源: 题型:
【题目】如图中的折线ABC表示某汽车的耗油量y(单位:L/km)与速度x(单位:km/h)之间的函数关系(30≤x≤120),已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
(1)当速度为50km/h、100km/h时,该汽车的耗油量分别为 L/km、 L/km.
(2)求线段AB所表示的y与x之间的函数表达式.
(3)速度是多少时,该汽车的耗油量最低?最低是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
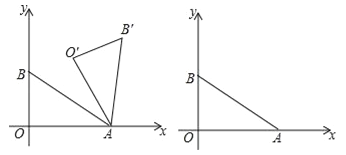
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 的图象与x轴、y轴分别交于点A、B,把Rt△AOB绕点A顺时针旋转角α(30°<α<180°),得到△AO′B′.
的图象与x轴、y轴分别交于点A、B,把Rt△AOB绕点A顺时针旋转角α(30°<α<180°),得到△AO′B′.
(1)当α=60°时,判断点B是否在直线O′B′上,并说明理由;
(2)连接OO′,设OO′与AB交于点D,当α为何值时,四边形ADO′B′是平行四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影: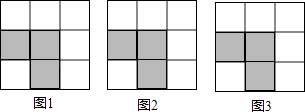
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从标号分别为1,2,3,4,5的5张卡片中,随机抽取1张,下列事件中,必然事件是( )
A. 该卡片标号小于6 B. 该卡片标号大于6
C. 该卡片标号是奇数 D. 该卡片标号是3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com