
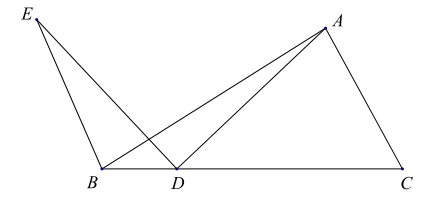
【题目】如图,在![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,将线段
上的动点,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .若已知
.若已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() 两点间的距离为
两点间的距离为![]() 两点间的距离为
两点间的距离为![]() .(若同学们打印的BC的长度如不是
.(若同学们打印的BC的长度如不是![]() ,请同学们重新画图、测量)
,请同学们重新画图、测量)
小明根据学习函数的经验,分别对![]() 自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整:
自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 7.03 | 6.20 | 5.44 | 4.76 | 4.21 | 3.85 | 3.73 | 3.87 | 4.26 |
|
| 5.66 | 4.32 |
| 1.97 | 1.59 | 2.27 | 3.43 | 4.73 |
写出![]() 的值.(保留1位小数)
的值.(保留1位小数)
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 的图象;
的图象;
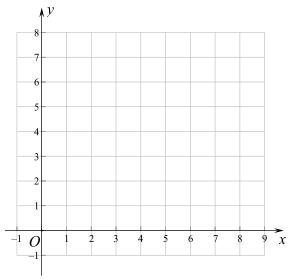
(3)结合函数图像,解决问题:
①当![]() 在线段
在线段![]() 上时,
上时,![]() 的长度约为________
的长度约为________![]() ;
;
②当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度
的长度![]() 约为_______
约为_______![]() .
.
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于A、B两点,点B坐标为(-4,-2),C为双曲线
交于A、B两点,点B坐标为(-4,-2),C为双曲线![]() 上一点,且在第一象限内,若△AOC面积为6,则点C坐标为( )
上一点,且在第一象限内,若△AOC面积为6,则点C坐标为( )
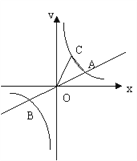
A. (4,2) B. (2,3) C. (3,4) D. (2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某植物园有一块足够大的空地,其中有一堵长为a米的墙,现准备用20米的篱笆围两间矩形花圃,中间用篱笆隔开.小俊设计了如图甲和乙的两种方案:
方案甲中AD的长不超过墙长;方案乙中AD的长大于墙长.
(1)若a=6.
①按图甲的方案,要围成面积为25平方米的花圃,则AD的长是多少米?
②按图乙的方案,能围成的矩形花圃的最大面积是多少?
(2)若0<a<6.5,哪种方案能围成面积最大的矩形花圃?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
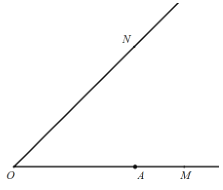
【题目】如图,已知![]() ,
,![]() 为射线
为射线![]() 上一定点,点
上一定点,点![]() 关于射线
关于射线![]() 的对称点为点
的对称点为点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,满足
,满足![]() 为钝角,以点
为钝角,以点![]() 为中心,将线段
为中心,将线段![]() 逆时针旋转
逆时针旋转![]() 至线段
至线段![]() ,满足点
,满足点![]() 在射线
在射线![]() 的反向延长线上.
的反向延长线上.
(1)依题意补全图形;
(2)当点![]() 在运动过程中,旋转角
在运动过程中,旋转角![]() 是否发生变化?若不变化,请求出
是否发生变化?若不变化,请求出![]() 的值,若变化,请说明理由;
的值,若变化,请说明理由;
(3)从点![]() 向射线
向射线![]() 作垂线,与射线
作垂线,与射线![]() 的反向延长线交于点
的反向延长线交于点![]() ,探究线段
,探究线段![]() 和
和![]() 的数量关系并证明.
的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
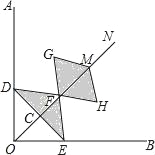
【题目】如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
A. y=![]() B. y=
B. y=![]() C. y=2
C. y=2![]() D. y=3
D. y=3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△BCD中,∠DCB=120°,点E满足∠DEC=60°.
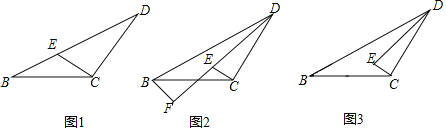
(1)如图1,点E在边BD上时,求证:ED=2BE;
(2)如图2,过点B作DE的垂线交DE的延长线于点F,试探究DE和EF的数量关系,并证明;
(3)若∠DEB=150°,直接写出BE,DE和EC的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了坚持以人民为中心的发展思想,以不断改善民生为发展的根本目的,某机构随机对某小区部分居民进行了关于“社区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表,根据图标信息,解答下列问题:
满意度 | 人数 | 所占百分比 |
非常满意 | 12 |
|
满意 | 54 |
|
比较满意 |
|
|
不满意 | 6 |
|
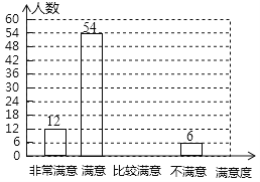
(1)本次调查的总人数为_______.
(2)请补全条形统计图;
(3)据统计,该社区服务站平均每天接待居民约1000名,若将“非常满意”和“消意”作为居民对社区服务站服务工作的肯定,请你估计该社区服务站服务工作平均每天得到多少名居民的肯定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=a(x﹣![]() )(x+3)交x轴于点A、B,交y轴于点C,tan∠CAO=
)(x+3)交x轴于点A、B,交y轴于点C,tan∠CAO=![]() .
.
(1)求a值;
(2)点P为第一象限内抛物线上一点,点P的横坐标为t,连接PA,PC,设△PAC的面积为S,求S与t之间的关系式;
(3)在(2)的条件下,点Q在第一象限内的抛物线上(点Q在点P的上方),过点P作PE⊥AB,垂足为E,点D在线段AQ上,点F在线段AO上连接ED、DF,DE交AP于点G,若∠QDF+∠QDE=180°,∠DFA+∠AED=90°,PG=PE,PG:EF=3:2,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com