
����Ŀ����ͼ1����֪ƽ���ı���ABCD����A������Ϊ��2��6������B��y���ϣ���AD��BC��x�ᣬ��B��C��D�����������y=ax2+bx+c��a��0���Ķ�������Ϊ��2��2������F��m��6�����߶�AD��һ���㣬ֱ��OF��BC�ڵ�E��
��1���������ߵı���ʽ��
��2�����ı���ABEF�����ΪS�������S��m�ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��3����ͼ2������F��FM��x�ᣬ����ΪM����ֱ��AC��P������P��PN��y�ᣬ����ΪN������MN��ֱ��AC�ֱ�x�ᣬy���ڵ�H��G�������߶�MN����Сֵ����ֱ��д����ʱm��ֵ��
���𰸡�
��1��
�⣺�߹�B��C��D�����������y=ax2+bx+c��a��0���Ķ�������Ϊ��2��2����
���C�ĺ�����Ϊ4��BC=4��
���ı���ABCDΪƽ���ı��Σ�
��AD=BC=4��
��A��2��6����
��D��6��6����
�������߽���ʽΪy=a��x��2��2+2��
�ߵ�D�ڴ��������ϣ�
��6=a��6��2��2+2��
��a= ![]() ��
��
�������߽���ʽΪy= ![]() ��x��2��2+2=
��x��2��2+2= ![]() x2��x+3
x2��x+3
��2��
�⣺��AD��BC��x�ᣬ��AD��BC��ľ���Ϊ3��BC��x��ľ���ҲΪ3��F��m��6��
��E�� ![]() ��3����
��3����
��BE= ![]() ��
��
��S= ![]() ��AF+BE����3=
��AF+BE����3= ![]() ��m��2+
��m��2+ ![]() ����3=
����3= ![]() m��3
m��3
�ߵ�F��m��6�����߶�AD�ϣ�
��2��m��6��
����S= ![]() m��3��2��m��6��
m��3��2��m��6��
��3��
�⣺����һ���������߽���ʽΪy= ![]() x2��x+3��
x2��x+3��
��B��0��3����C��4��3����
��A��2��6����
��ֱ��AC����ʽΪy=�� ![]() x+9��
x+9��
��FM��x�ᣬ����ΪM����ֱ��AC��P
��P��m���� ![]() m+9������2��m��6��
m+9������2��m��6��
��PN=m��PM=�� ![]() m+9��
m+9��
��FM��x�ᣬ����ΪM����ֱ��AC��P������P��PN��y�ᣬ
���MPN=90�㣬
��MN= ![]() =
= ![]() =
= ![]()
��2��m��6��
�൱m= ![]() ʱ��MN��С=
ʱ��MN��С= ![]() =
= ![]() ��
��
���������������߽���ʽΪy= ![]() x2��x+3��
x2��x+3��
��B��0��3����C��4��3����
��A��2��6����
��ֱ��AC����ʽΪy=�� ![]() x+9��
x+9��
��G��0��9����H��6��0����
��GH=3 ![]() ��
��
������֪���ı���NOMPΪ���Σ�
��MN=OP��
�൱OP��GHʱ��OP��̣���ΪMN��̣�
��S��GOH= ![]() OGOH=
OGOH= ![]() GHOP����
GHOP����
��9��6=3 ![]() ��OP����
��OP����
��OP��С= ![]() ��
��
����MN��СΪ ![]()
����������1������ƽ���ı��ε����ʺ������ߵ��ص�ȷ������D��Ȼ���ô���ϵ����ȷ���������ߵĽ���ʽ����2������AD��BC��x�ᣬ��AD��BC��ľ���Ϊ3��BC��x��ľ���ҲΪ3��F��m��6����ȷ����E�� ![]() ��3�����Ӷ�������ε��������3������һ�������ֱ��AC����ʽ��Ȼ�����FM��x�ᣬ��ʾ����P��m����
��3�����Ӷ�������ε��������3������һ�������ֱ��AC����ʽ��Ȼ�����FM��x�ᣬ��ʾ����P��m���� ![]() m+9���������ݹ��ɶ������MN=
m+9���������ݹ��ɶ������MN= ![]() ���Ӷ�ȷ����MN��Сֵ��m��ֵ��
���Ӷ�ȷ����MN��Сֵ��m��ֵ��
��������������֪���ı���NOMPΪ���Σ�MN=OP�����Ե�OP��GHʱ��OP��̣���ΪMN��̣�Ȼ�����������ε���������OP��Сֵ��
�����㾫����������Ҫ�����˶��κ�������ֵ�����֪ʶ�㣬��Ҫ��������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�����Ϊ16����D��BC����һ�㣬��BD= ![]() BC����G��AB��һ�㣬��B�ڡ�ABC�ڲ������ı���BDHG��ƽ���ı��Σ���ͼ����Ӱ���ֵ������ ��
BC����G��AB��һ�㣬��B�ڡ�ABC�ڲ������ı���BDHG��ƽ���ı��Σ���ͼ����Ӱ���ֵ������ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ��������5�����ۣ���abc��0����b��a+c����9a+3b+c��0�� ��c����3a�� ��a+b��m��am+b����������ȷ���У� �� 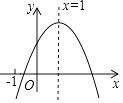
A.2��
B.3��
C.4��
D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѽ��ҹ������ºͳ��±��Ĵ�ͳ��ijУ��ѧ��ȤС��Ϊ���˽ⱾУѧ��ϲ���±�������������ȡ��60��ͬѧ�����ʾ����飬����ͳ�ƺ�����������в�������ͳ��ͼ�� 
��ע�������ʾ������ÿһλͬѧ���κ�һ�ַ���ͳ����ֻ��һ��ѡ��
�����ͳ��ͼ����������⣺
��1������ͳ��ͼ�У�����ϲ�����IJ�������Ӧ��Բ�Ľ�Ϊ�ȣ� ����ͳ��ͼ�У�ϲ������ɳ���±���ѧ�����ˣ�
��2������У����ѧ��900�ˣ���������������������Ƹ�Уѧ���С���ϲ�����͡��Ƚ�ϲ�����±��Ĺ����ˣ�
��3����ͬѧ��������±�����ͬѧ��Զ�ɳ�±���������������װ��ȫһ�������ȡ���ɳ�����ء����������±���һ�����üס���ÿ�˸�ѡһ�������û���״ͼ�����б���������ס�������������ֻ��һ��ѡ���Լ���Ե��±��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬��BCΪֱ���ġ�O��б��AB�ڵ�M����H��AC���е㣬����MH�� 
��1����֤��MHΪ��O�����ߣ�
��2����MH= ![]() ��tan��ABC=
��tan��ABC= ![]() �����O�İ뾶��
�����O�İ뾶��
��3���ڣ�2���������·ֱ����A��B����O�����ߣ������߽��ڵ�D��AD���O������N�㣬��N����NQ��BC������ΪE���ҽ���O��Q�㣬���߶�NQ�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y=x2��2mx��3�����н��۴�����ǣ� ��
A.����ͼ����x������������
B.����x2��2mx=3������֮��Ϊ��3
C.����ͼ��ĶԳ�����y����Ҳ�
D.x��mʱ��y��x���������С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AD��BC��CM�ǡ�BCD��ƽ���ߣ���CM��AB��MΪ���㣬AM= ![]() AB�����ı���ABCD�����Ϊ
AB�����ı���ABCD�����Ϊ ![]() �����ı���AMCD������� ��
�����ı���AMCD������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��˳����������Ϊ2�ĵ���ֱ�������θ����е�õ���1��С�����Σ���˳���������õ�С�����θ����е�õ���2��С�����Σ���˲�����ȥ�����n��С�����ε����Ϊ �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com