Question

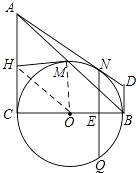
【题目】如图，在Rt△ABC中，∠C=90°，以BC为直径的⊙O交斜边AB于点M，若H是AC的中点，连接MH．
（1）求证：MH为⊙O的切线．
（2）若MH= ，tan∠ABC= ，求⊙O的半径．
（3）在（2）的条件下分别过点A、B作⊙O的切线，两切线交于点D，AD与⊙O相切于N点，过N点作NQ⊥BC，垂足为E，且交⊙O于Q点，求线段NQ的长度．

Answer 1

【答案】
（1）证明：连接OH、OM，

∵H是AC的中点，O是BC的中点，

∴OH是△ABC的中位线，

∴OH∥AB，

∴∠COH=∠ABC，∠MOH=∠OMB，

又∵OB=OM，

∴∠OMB=∠MBO，

∴∠COH=∠MOH，

在△COH与△MOH中，

，

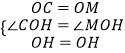∴△COH≌△MOH（SAS），

∴∠HCO=∠HMO=90°，

∴MH是⊙O的切线

（2）解：∵MH、AC是⊙O的切线，

∴HC=MH= ，

∴AC=2HC=3，

∵tan∠ABC= ，

∴ = ，

∴BC=4，

∴⊙O的半径为2

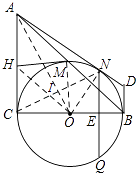
（3）解：连接OA、CN、ON，OA与CN相交于点I，

∵AC与AN都是⊙O的切线，

∴AC=AN，AO平分∠CAD，

∴AO⊥CN，

∵AC=3，OC=2，

∴由勾股定理可求得：AO= ，

∵ ACOC= AOCI，

∴CI= ，

∴由垂径定理可求得：CN= ，

设OE=x，

由勾股定理可得：CN2﹣CE2=ON2﹣OE2，

∴ ﹣（2+x）2=4﹣x2，

∴x= ，

∴OE= ，

由勾股定理可求得：EN= ，

∴由垂径定理可知：NQ=2EN= ．

【解析】（1）连接OH、OM，易证OH是△ABC的中位线，利用中位线的性质可证明△COH≌△MOH，所以∠HCO=∠HMO=90°，从而可知MH是⊙O的切线；（2）由切线长定理可知：MH=HC，再由点M是AC的中点可知AC=3，由tan∠ABC= ，所以BC=4，从而可知⊙O的半径为2；（3）连接CN，AO，CN与AO相交于I，由AC、AN是⊙O的切线可知AO⊥CN，利用等面积可求出可求得CI的长度，设CE为x，然后利用勾股定理可求得CE的长度，利用垂径定理即可求得NQ．