
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,且经过点A(0, ![]() )
)
(1)若此抛物线经过点B(2,﹣ ![]() ),且与x轴相交于点E,F.
),且与x轴相交于点E,F.
①填空:b=(用含a的代数式表示);
(2)若a= ![]() ,当0<x<1,抛物线上的点到x轴距离的最大值为3时,求b的值.
,当0<x<1,抛物线上的点到x轴距离的最大值为3时,求b的值.
【答案】
(1)[ "﹣2a﹣1
②当EF2的值最小时,求抛物线的解析式;
解:由①可得抛物线解析式为y=ax2﹣(2a+1)x+ ![]() ,
,
令y=0可得ax2﹣(2a+1)x+ ![]() =0,
=0,
∵△=(2a+1)2﹣4a× ![]() =4a2﹣2a+1=4(a﹣
=4a2﹣2a+1=4(a﹣ ![]() )2+
)2+ ![]() >0,
>0,
∴方程有两个不相等的实数根,设为x1、x2 ,
∴x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
∴EF2=(x1﹣x2)2=(x1+x2)2﹣4x1x2= ![]() =(
=( ![]() ﹣1)2+3,
﹣1)2+3,
∴当a=1时,EF2有最小值,即EF有最小值,
∴抛物线解析式为y=x2﹣3x+ ![]() (2)
(2)
解:当a= ![]() 时,抛物线解析式为y=
时,抛物线解析式为y= ![]() x2+bx+
x2+bx+ ![]() ,
,
∴抛物线对称轴为x=﹣b,
∴只有当x=0、x=1或x=﹣b时,抛物线上的点才有可能离x轴最远,
当x=0时,y= ![]() ,当x=1时,y=
,当x=1时,y= ![]() +b+
+b+ ![]() =2+b,当x=﹣b时,y=
=2+b,当x=﹣b时,y= ![]() (﹣b)2+b(﹣b)+
(﹣b)2+b(﹣b)+ ![]() =﹣
=﹣ ![]() b2+
b2+ ![]() ,
,
①当|2+b|=3时,b=1或b=﹣5,且顶点不在0<x<1范围内,满足条件;
②当|﹣ ![]() b2+
b2+ ![]() |=3时,b=±3,对称轴为直线x=±3,不在0<x<1范围内,故不符合题意,
|=3时,b=±3,对称轴为直线x=±3,不在0<x<1范围内,故不符合题意,
综上可知b的值为1或﹣5
【解析】解:(1.)①∵抛物线y=ax2+bx+c的开口向上,且经过点A(0, ![]() ),
),
∴c= ![]() ,
,
∵抛物线经过点B(2,﹣ ![]() ),
),
∴﹣ ![]() =4a+2b+
=4a+2b+ ![]() ,
,
∴b=﹣2a﹣1,
所以答案是:﹣2a﹣1;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH. 
(1)求证:MH为⊙O的切线.
(2)若MH= ![]() ,tan∠ABC=
,tan∠ABC= ![]() ,求⊙O的半径.
,求⊙O的半径.
(3)在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于N点,过N点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段NQ的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)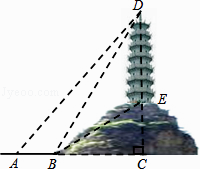
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D是直径为AB的⊙O上的四个点,C是劣弧 ![]() 的中点,AC与BD交于点E.
的中点,AC与BD交于点E. 
(1)求证:DC2=CEAC;
(2)若AE=2,EC=1,求证:△AOD是正三角形;
(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,求△ACH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现在平均每天比原计划多生产25个零件,现在生产600个零件所需时间与原计划生产450个零件所需时间相同,原计划平均每天生产多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顺次连接腰长为2的等腰直角三角形各边中点得到第1个小三角形,再顺次连接所得的小三角形各边中点得到第2个小三角形,如此操作下去,则第n个小三角形的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点. 
(1)求证:DE=DC;
(2)求证:AF⊥BF;
(3)当AFGF=28时,请直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如下,则一次函数y=ax﹣2b与反比例函数y= ![]() 在同一平面直角坐标系中的图象大致是( )
在同一平面直角坐标系中的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com