Question

【题目】如图，点A，B，C，D是直径为AB的⊙O上的四个点，C是劣弧 的中点，AC与BD交于点E．
（1）求证：DC2=CEAC；
（2）若AE=2，EC=1，求证：△AOD是正三角形；
（3）在（2）的条件下，过点C作⊙O的切线，交AB的延长线于点H，求△ACH的面积．

Answer 1

【答案】
（1）证明：∵C是劣弧 的中点，

∴∠DAC=∠CDB，

∵∠ACD=∠DCE，

∴△ACD∽△DCE，

∴ = ，

∴DC2=CEAC

（2）证明：∵AE=2，EC=1，

∴AC=3，

∴DC2=CEAC=1×3=3，

∴DC= ，

连接OC、OD，如图所示：

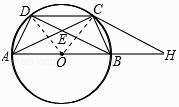
∵C是劣弧 的中点，

∴OC平分∠DOB，BC=DC= ，

∵AB是⊙O的直径，

∴∠ACB=90°，

∴AB= =2 ，

∴OB=OC=OD=DC=BC= ，

∴△OCD、△OBC是正三角形，

∴∠COD=∠BOC=∠OBC=60°，

∴∠AOD=180°﹣2×60°=60°，

∵OA=OD，

∴△AOD是正三角形

（3）解：∵CH是⊙O的切线，∴OC⊥CH，

∵∠COH=60°，

∴∠H=30°，

∵∠BAC=90°﹣60°=30°，

∴∠H=∠BAC，

∴AC=CH=3，

∵AH=3 ，AH上的高为BCsin60°= ，

∴△ACH的面积= ×3 × =

【解析】（1）由圆周角定理得出∠DAC=∠CDB，证明△ACD∽△DCE，得出对应边成比例，即可得出结论；（2）求出DC= ，连接OC、OD，如图所示：证出BC=DC= ，由圆周角定理得出∠ACB=90°，由勾股定理得出AB= =2 ，得出OB=OC=OD=DC=BC= ，证出△OCD、△OBC是正三角形，得出∠COD=∠BOC=∠OBC=60°，求出∠AOD=60°，即可得出结论；（3）由切线的性质得出OC⊥CH，求出∠H=30°，证出∠H=∠BAC，得出AC=CH=3，求出AH和高，由三角形面积公式即可得出答案．