Question

【题目】如图，在ABCD中，BE⊥AC，垂足E在CA的延长线上，DF⊥AC，垂足F在AC的延长线上，求证：AE=CF．

Answer 1

【答案】证明：∵四边形ABCD是平行四边形， ∴AB∥CD，AB=CD，
∴∠BAC=∠DCA，
∴180°﹣∠BAC=180°﹣∠DCA，
∴∠EAB=∠FAD，
∵BE⊥AC，DF⊥AC，
∴∠BEA=∠DFC=90°，
在△BEA和△DFC中， ，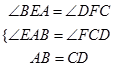
∴△BEA≌△DFC（AAS），
∴AE=CF
【解析】由平行四边形的性质得出AB∥CD，AB=CD，由平行线的性质得出得出∠BAC=∠DCA，证出∠EAB=∠FAD，∠BEA=∠DFC=90°，由AAS证明△BEA≌△DFC，即可得出结论．
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．