
����Ŀ�������л�ʫ�ʣ�Ѱ�Ļ�����Ʒ����֮������ijУ�ٰ����조�й�ʫ�ʴ�ᡱ����ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱĬд50��ʫ�ʣ���ÿ��ȷĬд��һ��ʫ�ʵ�2�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 50��x��60 | 6 |
��2�� | 60��x��70 | 8 |
��3�� | 70��x��80 | 14 |
��4�� | 80��x��90 | a |
��5�� | 90��x��100 | 10 |
����ͼ��������и��⣺
��1���������a��ֵ����Ƶ���ֲ�ֱ��ͼ����������
��2�������Գɼ�������80��Ϊ���㣬�β��Ե��������Ƕ��٣�
��3����5��10��ͬѧ�У���4����ͬѧ���ֽ���10��ͬѧƽ���ֳ�������жԿ���ϰ����4����ͬѧÿ������ˣ���С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ�
���𰸡�
��1���⣺��������ͱ��ɵ�
a=50��6��8��14��10=12��
��a��ֵ��12��
�ڲ���������Ƶ���ֲ�ֱ��ͼ����ͼ��ʾ��
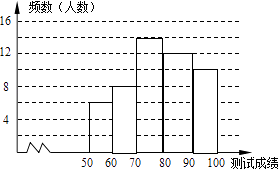
��2���⣺�߲��Գɼ�������80��Ϊ���㣬
�౾�β��Ե��������ǣ� ![]()
��3���⣺��С����Сǿ�ֱ�ΪA��B����������ѧ��Ϊ��C��D��
�����еĿ�����Ϊ����AB������AC������AD������BA������BC������BD������CA������CB������CD������DA������DB������DC����
����С����Сǿ����һ��ĸ���Ϊ�� ![]()
����������1���ٸ�������ͱ��е����ݿ������a��ֵ�����ɱ����е����ݿ��Խ�Ƶ���ֲ���������������2�����ݱ����е����ݺͲ��Գɼ�������80��Ϊ���㣬������������ʣ���3�������������������еĿ����ԣ��Ӷ����Եõ�С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ�
�����㾫����������Ĺؼ���������Ƶ���ֲ�ֱ��ͼ�����֪ʶ�������ص㣺��������ʾ�����Ƶ���ֲ��������������ʾ�����Ƶ����𣮣�ע����������ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ�����Լ����б�������״ͼ�������⣬�˽һ������Ҫ�����������������ʱ�����б����Ͳ������ˣ�Ϊ�˲��ز�©���г����п��ܵĽ����ͨ��������״ͼ������ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѵ�С��ȫ��ͬ��6��ƹ����ֳ����飬ÿ��3����ÿ��ƹ��������ֱ��������1��2��3����������ƹ����ֱ�������������н��ȣ��ٴ�ÿ�������и����ȡ��1��ƹ�������û���״ͼ�����б����ķ�������ȡ����2��ƹ������������֮��Ϊż���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��̣�a+c��x2+2bx+��a��c��=0������a��b��c�ֱ�Ϊ ![]() ���ߵij���
���ߵij���
��1����� ![]() �Ƿ��̵ĸ�����
�Ƿ��̵ĸ����� ![]() ����״Ϊ ��
����״Ϊ ��
��2�����������������ȵ�ʵ���������ж� ![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��3����� ![]() �ǵȱ������Σ��������һԪ���η��̵ĸ���
�ǵȱ������Σ��������һԪ���η��̵ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڷ�װ�����4����4000Ԫ������һ��������ɼ������к�ܿ����꣬��װ����5�³��ֹ���ͬ�������ĸÿ���£����ڵڶ������½���ʱ�۸�ȵ�һ�����½���ʱ�۸������20Ԫ������ڶ������½�������5000Ԫ��
��1����һ�����½���ʱ�ļ۸��Ƕ��٣�
��2����һ�������ۼ�Ϊ120Ԫ/����Ϊ��֤�ڶ������µ������ʲ����ڵ�һ�����µ������ʣ���ô�ڶ�������ÿ���ۼ������Ƕ���Ԫ�� ����ʾ������=�ۼ۩��ɱ���������= ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�����Ϊ16����D��BC����һ�㣬��BD= ![]() BC����G��AB��һ�㣬��B�ڡ�ABC�ڲ������ı���BDHG��ƽ���ı��Σ���ͼ����Ӱ���ֵ������ ��
BC����G��AB��һ�㣬��B�ڡ�ABC�ڲ������ı���BDHG��ƽ���ı��Σ���ͼ����Ӱ���ֵ������ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������ABCD�У���MAN=45�㣬��MAN�Ƶ�A˳ʱ����ת���������߷ֱ�CB��DC�������ǵ��ӳ��ߣ��ڵ�M��N��AH��MN�ڵ�H�� 
��1����ͼ�٣�����MAN�Ƶ�A��ת��BM=DNʱ������ֱ��д��AH��AB��������ϵ����
��2����ͼ�ڣ�����MAN�Ƶ�A��ת��BM��DNʱ����1���з��ֵ�AH��AB��������ϵ�������������������д�����ɣ����������֤����
��3����ͼ�ۣ���֪��MAN=45�㣬AH��MN�ڵ�H����MH=2��NH=3����AH�ij����������ã�2���õ��Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�У���C=90�㣬��P��CD���ϵĶ��㣬����AP��E��F�ֱ���AB��AP���е㣬����P��CD�ϴӵ�D���C�ƶ������У����н��۳������ǣ� �� 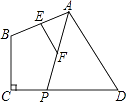
A.�߶�EF�ij��ȼ�С������
B.�߶�EF�ij�����
C.�߶�EF�ij�������
D.�߶�EF�ij���С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬��BCΪֱ���ġ�O��б��AB�ڵ�M����H��AC���е㣬����MH�� 
��1����֤��MHΪ��O�����ߣ�
��2����MH= ![]() ��tan��ABC=
��tan��ABC= ![]() �����O�İ뾶��
�����O�İ뾶��
��3���ڣ�2���������·ֱ����A��B����O�����ߣ������߽��ڵ�D��AD���O������N�㣬��N����NQ��BC������ΪE���ҽ���O��Q�㣬���߶�NQ�ij��ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com