Question

【题目】已知，正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，AH⊥MN于点H．
（1）如图①，当∠MAN绕点A旋转到BM=DN时，请你直接写出AH与AB的数量关系：；
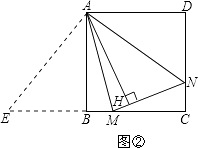
（2）如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；
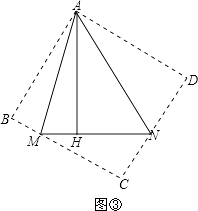
（3）如图③，已知∠MAN=45°，AH⊥MN于点H，且MH=2，NH=3，求AH的长．（可利用（2）得到的结论）

Answer 1

【答案】
（1）AH=AB
（2）数量关系成立．如图②，延长CB至E，使BE=DN．

∵ABCD是正方形，

∴AB=AD，∠D=∠ABE=90°，

在Rt△AEB和Rt△AND中， ，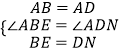

∴Rt△AEB≌Rt△AND，

∴AE=AN，∠EAB=∠NAD，

∴∠EAM=∠NAM=45°，

在△AEM和△ANM中， ，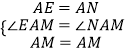

∴△AEM≌△ANM．

∴S△AEM=S△ANM，EM=MN，

∵AB、AH是△AEM和△ANM对应边上的高，

∴AB=AH．

（3）如图③分别沿AM、AN翻折△AMH和△ANH，得到△ABM和△AND，

∴BM=2，DN=3，∠B=∠D=∠BAD=90°．

分别延长BM和DN交于点C，得正方形ABCD，

由（2）可知，AH=AB=BC=CD=AD．

设AH=x，则MC=x﹣2，NC=x﹣3，

在Rt△MCN中，由勾股定理，得MN2=MC2+NC2

∴52=（x﹣2）2+（x﹣3）2（6分）

解得x1=6，x2=﹣1．（不符合题意，舍去）

∴AH=6．

【解析】解：（1）如图①AH=AB． （1）由三角形全等可以证明AH=AB，（2）延长CB至E，使BE=DN，证明△AEM≌△ANM，能得到AH=AB，（3）分别沿AM、AN翻折△AMH和△ANH，得到△ABM和△AND，然后分别延长BM和DN交于点C，得正方形ABCE，设AH=x，则MC=x﹣2，NC=x﹣3，在Rt△MCN中，由勾股定理，解得x．