
°æƒø°ø”–“ªøÈ∫¨30°„Ω«µƒ÷±Ω«»˝Ω«∞ÂOMN£¨∆‰÷–°œMON£Ω90°„£¨°œNMO£Ω30°„£¨ON£Ω2![]() £¨Ω´’‚øÈ÷±Ω«»˝Ω«∞Â∞¥»ÁÕºÀ˘ 挪÷√∞⁄∑≈£Æµ»±þ°˜ABCµƒ∂•µ„B”ε„O÷ÿ∫œ£¨BC±þ¬‰‘⁄OM…œ£¨µ„A«°∫√¬‰‘⁄–±±þMN…œ£¨Ω´µ»±þ°˜ABC¥”Õº1µƒŒª÷√—ÿOM∑ΩœÚ“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»∆Ω“∆£¨±þAB£¨AC∑÷±”Ζ±±þMNΩª”⁄µ„E£¨F£®»ÁÕº2À˘ 棩£¨…Ë°˜ABC∆Ω“∆µƒ ±º‰Œ™t£®s£©£®0£ºt£º6£©£Æ
£¨Ω´’‚øÈ÷±Ω«»˝Ω«∞Â∞¥»ÁÕºÀ˘ 挪÷√∞⁄∑≈£Æµ»±þ°˜ABCµƒ∂•µ„B”ε„O÷ÿ∫œ£¨BC±þ¬‰‘⁄OM…œ£¨µ„A«°∫√¬‰‘⁄–±±þMN…œ£¨Ω´µ»±þ°˜ABC¥”Õº1µƒŒª÷√—ÿOM∑ΩœÚ“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»∆Ω“∆£¨±þAB£¨AC∑÷±”Ζ±±þMNΩª”⁄µ„E£¨F£®»ÁÕº2À˘ 棩£¨…Ë°˜ABC∆Ω“∆µƒ ±º‰Œ™t£®s£©£®0£ºt£º6£©£Æ
£®1£©µ»±þ°˜ABCµƒ±þ≥§Œ™°° °°£ª
£®2£©‘⁄‘À∂Øπ˝≥Ã÷–£¨µ±°° °° ±£¨MN¥π÷±∆Ω∑÷AB£ª
£®3£©µ±0£ºt£º6 ±£¨«Û÷±Ω«»˝Ω«∞ÂOMN”ε»±þ°˜ABC÷ÿµ˛≤ø∑÷µƒ√ʪ˝S”Î ±º‰t÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£Æ
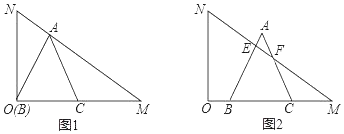
°æ¥∞∏°ø£®1£©3£ª£®2£©3£ª£®3£©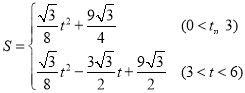 .
.
°æΩ‚Œˆ°ø
£®1£©∏˘æ𣨰œOMN£Ω30°„∫Õ°˜ABCŒ™µ»±þ»˝Ω«–Œ£¨«Û÷§°˜OAMŒ™÷±Ω«»˝Ω«–Œ£¨»ª∫Ûº¥ø…µ√≥ˆ¥∞∏£Æ
£®2£©“◊÷™µ±µ„C”ÎM÷ÿ∫œ ±÷±œþMN∆Ω∑÷œþ∂ŒAB£¨¥À ±OB£Ω3£¨”…¥Àº¥ø…Ω‚æˆŒ £ª
£®3£©∑÷¡Ω÷÷«È–Œ∑÷±«ÛΩ‚£∫µ±0£ºt°Ð3 ±£¨◊˜CD°ÕFM”⁄D£Æ∏˘æðS£ΩS°˜MEB©Å2S°˜MDC£¨º∆À„º¥ø…£Æ¢⁄µ±3£ºt£º6 ±£¨S£ΩS°˜MEB£Æ
Ω‚£∫£®1£©‘⁄Rt°˜MON÷–£¨°þ°œMON£Ω90°„£¨ON£Ω2![]() £¨°œM£Ω30°„
£¨°œM£Ω30°„
°ýOM£Ω![]() ON£Ω6£¨
ON£Ω6£¨
°þ°˜ABCŒ™µ»±þ»˝Ω«–Œ
°ý°œAOC£Ω60°„£¨
°ý°œOAM£Ω90°„
°ýOA°ÕMN£¨º¥°˜OAMŒ™÷±Ω«»˝Ω«–Œ£¨
°ýOA£Ω![]() OM£Ω
OM£Ω![]() °¡6£Ω3£Æ
°¡6£Ω3£Æ
π ¥∞∏Œ™3£Æ
£®2£©“◊÷™µ±µ„C”ÎM÷ÿ∫œ ±÷±œþMN∆Ω∑÷œþ∂ŒAB£¨¥À ±OB£Ω3£¨À˘“‘t£Ω3£Æ
π ¥∞∏Œ™3£Æ
£®3£©“◊÷™£∫OM£Ω6£¨MN£Ω4![]() £¨S°˜OMN£Ω
£¨S°˜OMN£Ω![]() °¡2
°¡2![]() °¡6£Ω6
°¡6£Ω6![]() £¨
£¨
°þ°œM£Ω30°„£¨°œMBA£Ω60°„£¨
°ý°œBEM£Ω90°„£Æ
¢Ÿµ±0£ºt°Ð3 ±£¨◊˜CD°ÕFM”⁄D£Æ
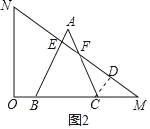
°þ°œACB£Ω60°„£¨°œM£Ω30°„£¨°œFCB£Ω°œM+°œCFM£¨
°ý°œCFM£Ω°œM£Ω30°„£¨
°ýCF£ΩCM£¨
°þCD°ÕFM£¨
°ýDF£ΩDM£¨
°ýS°˜CMF£Ω2S°˜CDM£¨
°þ°˜MEB°◊°˜MON£¨
°ý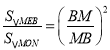 £¨
£¨
°ýS°˜MEB£Ω![]() £¨
£¨
°þ°˜MDC°◊°˜MON£¨
°ý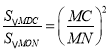 £¨
£¨
°ýS°˜MDC£Ω![]() £¨
£¨![]()
°ýS£ΩS°˜MEB©Å2S°˜MDC£Ω©Å![]() £Æ
£Æ
¢⁄µ±3£ºt£º6 ±£¨S£ΩS°˜MEB£Ω![]() £¨
£¨
◊€…œÀ˘ ˆ£¨S£Ω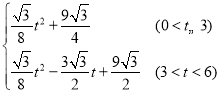 £Æ
£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø’˝∑Ω–ŒA1B1C1O£¨A2B2C2C1£¨A3B3C3C2£¨°≠∞¥»ÁÕºµƒ∑Ω Ω∑≈÷√£¨µ„A1£¨A2£¨A3°≠∫Õµ„C1£¨C2£¨C3°≠∑÷±‘⁄÷±œþy=x+1∫Õx÷·…œ£¨‘Úµ„Bnµƒ◊¯±ÍŒ™_____£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø¥Û÷⁄∑˛◊∞µÍΩÒƒÍ4‘¬”√4000‘™π∫Ω¯¡À“ªøÓ≥ƒ“¬»Ù∏…º˛£¨…œ –∫Û∫ÐøÏ €ÕÍ£¨∑˛◊∞µÍ”⁄5‘¬≥ı”÷π∫Ω¯∏√øÓ≥ƒ“¬£¨Ω¯ªı¡ø±»µ⁄“ª≈˙‘ˆº”¡À20%£¨”…”⁄µ⁄∂˛≈˙≥ƒ“¬Ω¯ªı ±º€∏Ò±»µ⁄“ª≈˙≥ƒ“¬Ω¯ªı ±º€∏Ò÷∏þ¡À20‘™£¨Ω·π˚µ⁄∂˛≈˙≥ƒ“¬Ω¯ªı”√¡À6000‘™
£®1£©µ⁄“ª≈˙≥ƒ“¬Ω¯ªı ±º€∏Ò «∂ý…Ÿ£ø
£®2£©µ⁄“ª≈˙≥ƒ“¬ €º€Œ™120‘™/º˛£¨Œ™±£÷§µ⁄∂˛≈˙≥ƒ“¬µƒ¿˚»Û¬ ≤ªµÕ”⁄µ⁄“ª≈˙≥ƒ“¬µƒ¿˚»Û¬ £¨ƒ«√¥µ⁄∂˛≈˙≥ƒ“¬√øº˛ €º€÷¡…Ÿ «∂ý…Ÿ‘™£ø£®Ã· æ£∫¿˚»Û£Ω €º€©Å≥…±æ£¨¿˚»Û¬ £Ω¿˚»Û°¬≥…±æ°¡100%£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
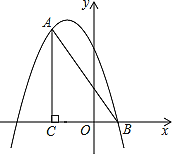
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨°œACB=90°„£¨OC=2OB£¨tan°œABC=2£¨µ„Bµƒ◊¯±ÍŒ™£®1£¨0£©£Æ≈◊ŒÔœþy=©Åx2+bx+cæ≠π˝A°¢B¡Ωµ„£Æ
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©µ„P «÷±œþAB…œ∑Ω≈◊ŒÔœþ…œµƒ“ªµ„£¨π˝µ„P◊˜PD¥π÷±x÷·”⁄µ„D£¨Ωªœþ∂ŒAB”⁄µ„E£¨ πPE=![]() DE£Æ
DE£Æ
¢Ÿ«Ûµ„Pµƒ◊¯±Í£ª
¢⁄‘⁄÷±œþPD…œ «∑ҥʑ⁄µ„M£¨ π°˜ABMŒ™÷±Ω«»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Û≥ˆ∑˚∫œÃıº˛µƒÀ˘”–µ„Mµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
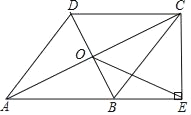
°æƒø°ø»ÁÕº£¨‘⁄Àƒ±þ–ŒABCD÷–£¨AB°ŒDC£¨AB£ΩAD£¨∂‘Ω«œþAC£¨BDΩª”⁄µ„O£¨AC∆Ω∑÷°œBAD£¨π˝µ„C◊˜CE°ÕABΩªABµƒ—”≥§œþ”⁄µ„E£¨¡¨Ω”OE£Æ
£®1£©«Û÷§£∫Àƒ±þ–ŒABCD «¡‚–Œ£ª
£®2£©»ÙAB£Ω![]() £¨BD£Ω2£¨«ÛOEµƒ≥§£Æ
£¨BD£Ω2£¨«ÛOEµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø”–“ªøÈ∫¨30°„Ω«µƒ÷±Ω«»˝Ω«∞ÂOMN£¨∆‰÷–°œMON£Ω90°„£¨°œNMO£Ω30°„£¨ON£Ω2![]() £¨Ω´’‚øÈ÷±Ω«»˝Ω«∞Â∞¥»ÁÕºÀ˘ 挪÷√∞⁄∑≈£Æµ»±þ°˜ABCµƒ∂•µ„B”ε„O÷ÿ∫œ£¨BC±þ¬‰‘⁄OM…œ£¨µ„A«°∫√¬‰‘⁄–±±þMN…œ£¨Ω´µ»±þ°˜ABC¥”Õº1µƒŒª÷√—ÿOM∑ΩœÚ“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»∆Ω“∆£¨±þAB£¨AC∑÷±”Ζ±±þMNΩª”⁄µ„E£¨F£®»ÁÕº2À˘ 棩£¨…Ë°˜ABC∆Ω“∆µƒ ±º‰Œ™t£®s£©£®0£ºt£º6£©£Æ
£¨Ω´’‚øÈ÷±Ω«»˝Ω«∞Â∞¥»ÁÕºÀ˘ 挪÷√∞⁄∑≈£Æµ»±þ°˜ABCµƒ∂•µ„B”ε„O÷ÿ∫œ£¨BC±þ¬‰‘⁄OM…œ£¨µ„A«°∫√¬‰‘⁄–±±þMN…œ£¨Ω´µ»±þ°˜ABC¥”Õº1µƒŒª÷√—ÿOM∑ΩœÚ“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»∆Ω“∆£¨±þAB£¨AC∑÷±”Ζ±±þMNΩª”⁄µ„E£¨F£®»ÁÕº2À˘ 棩£¨…Ë°˜ABC∆Ω“∆µƒ ±º‰Œ™t£®s£©£®0£ºt£º6£©£Æ
£®1£©µ»±þ°˜ABCµƒ±þ≥§Œ™°° °°£ª
£®2£©‘⁄‘À∂Øπ˝≥Ã÷–£¨µ±°° °° ±£¨MN¥π÷±∆Ω∑÷AB£ª
£®3£©µ±0£ºt£º6 ±£¨«Û÷±Ω«»˝Ω«∞ÂOMN”ε»±þ°˜ABC÷ÿµ˛≤ø∑÷µƒ√ʪ˝S”Î ±º‰t÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£Æ
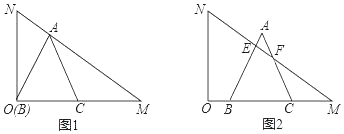
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£ ˝—ß–À»§–°◊ȵƒÕ¨—ß≤‚¡ø“ªºÐŒÞ»À∑…ª˙Pµƒ∏þ∂»£¨»ÁÕº£¨A£¨B¡Ω∏ˆπ€≤‚µ„œýæý![]() £¨‘⁄A¥¶≤‚µ√P‘⁄±±∆´∂´71°„∑ΩœÚ…œ£¨Õ¨ ±‘⁄B¥¶≤‚µ√P‘⁄±±∆´∂´35°„∑ΩœÚ…œ£Æ«ÛŒÞ»À∑…ª˙P¿Îµÿ√ʵƒ∏þ∂».(Ω·π˚æ´»∑µΩ1√◊£¨≤Œøº ˝æð£∫
£¨‘⁄A¥¶≤‚µ√P‘⁄±±∆´∂´71°„∑ΩœÚ…œ£¨Õ¨ ±‘⁄B¥¶≤‚µ√P‘⁄±±∆´∂´35°„∑ΩœÚ…œ£Æ«ÛŒÞ»À∑…ª˙P¿Îµÿ√ʵƒ∏þ∂».(Ω·π˚æ´»∑µΩ1√◊£¨≤Œøº ˝æð£∫![]() £¨
£¨![]() £¨sin71°„°÷0.95£¨tan71°„°÷2.90)
£¨sin71°„°÷0.95£¨tan71°„°÷2.90)

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫»ÁÕº,‘⁄¡‚–ŒABCD÷–,FŒ™±þABµƒ÷–µ„,DF”Î∂‘Ω«œþACΩª”⁄µ„G,π˝G◊˜GE°ÕAD”⁄µ„E,»ÙAB=2,«“°œ1=°œ2,‘Úœ¬¡–Ω·¬€£∫¢ŸDF°ÕAB;¢⁄CG=3GA;¢€CG=DF+GE;¢ÐSÀƒ±þ–ŒBFGC=![]() 1÷–,Àµ∑®’˝»∑µƒ «( )
1÷–,Àµ∑®’˝»∑µƒ «( )

A. ¢Ÿ¢€¢ÐB. ¢⁄¢€C. ¢Ÿ¢€D. ¢Ÿ¢⁄¢€
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øµ»—¸°˜ABC÷–£¨AB£ΩBC£Ω8£¨°œABC£Ω120°„£¨BE «°œABCµƒ∆Ω∑÷œþ£¨ΩªAC”⁄E£¨µ„D «ABµƒ÷–µ„£¨¡¨Ω”DE£¨◊˜EF°ŒAB”⁄µ„F£Æ
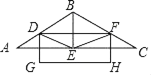
£®1£©«Û÷§Àƒ±þ–ŒBDEF «¡‚–Œ£ª
£®2£©»ÁÕº“‘DFŒ™“ª±þ◊˜æÿ–ŒDFHG£¨«“µ„E «¥Àæÿ–Œµƒ∂‘≥∆÷––ƒ£¨«Ûæÿ–Œ¡Ì“ª±þµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com