
【题目】已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论:①DF⊥AB;②CG=3GA;③CG=DF+GE;④S四边形BFGC=![]() 1中,说法正确的是( )
1中,说法正确的是( )

A. ①③④B. ②③C. ①③D. ①②③
【答案】C
【解析】
①由四边形ABCD是菱形,得出对角线平分对角,求得∠GAD=∠2,得出AG=GD,AE=ED,由SAS证得△AFG≌△AEG,得出∠AFG=∠AEG=90°,即可得出①正确;
②由DF⊥AB,F为边AB的中点,证得AD=BD,证出△ABD为等边三角形,得出∠BAC=∠1=∠2=30°,由AC=2ABcos∠BAC,AG= ![]() ,求出AC,AG,即可得出②不正确;
,求出AC,AG,即可得出②不正确;
③由勾股定理求出DF= ![]() ,由GE=tan∠2ED求出GE,即可得出③正确;
,由GE=tan∠2ED求出GE,即可得出③正确;
④由S四边形BFGC=S△ABC-S△AGF求出数值,即可得出④不正确.
∵四边形ABCD是菱形,
∴∠FAG=∠EAG,∠1=∠GAD,AB=AD,
∵∠1=∠2,
∴∠GAD=∠2,
∴AG=GD,
∵GE⊥AD,
∴GE垂直平分AD,
∴AE=ED,
∵F为边AB的中点,
∴AF=AE,
在△AFG和△AEG中,
 ,
,
∴△AFG≌△AEG(SAS),
∴∠AFG=∠AEG=90°,
∴DF⊥AB,
∴①正确;
连接BD.
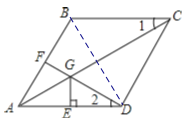
∵DF⊥AB,F为边AB的中点,
∴AF=![]() AB=1,AD=BD,
AB=1,AD=BD,
∵AB=AD,
∴AD=BD=AB,
∴△ABD为等边三角形,
∴∠BAD=∠BCD=60°,
∴∠BAC=∠1=∠2=30°,
∴AC=2ABcos∠BAC=2×2×![]() ,
,
AG=  ,
,
∴CG=AC-AG=![]()
![]() ,
,
∴CG=2GA,
∴②不正确;
∵GE垂直平分AD,
∴ED=![]() AD=1,
AD=1,
由勾股定理得:DF= ![]() ,
,
GE=tan∠2ED=tan30°×1=![]() ,
,
∴DF+GE= ![]()
∴③正确;
∵∠BAC=∠1=30°,
∴△ABC的边AC上的高等于AB的一半,即为1,
FG= ![]() ,
,
S四边形BFGC=S△ABC-S△AGF= ![]() ,
,
∴④不正确;
故选:C


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC=16.点D在边BC上,且点D到边AB和边AC的距离相等.
(1)用直尺和圆规作出点D(不写作法,保留作图痕迹,在图上标注出点D);
(2)求点D到边AB的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块含30°角的直角三角板OMN,其中∠MON=90°,∠NMO=30°,ON=2![]() ,将这块直角三角板按如图所示位置摆放.等边△ABC的顶点B与点O重合,BC边落在OM上,点A恰好落在斜边MN上,将等边△ABC从图1的位置沿OM方向以每秒1个单位长度的速度平移,边AB,AC分别与斜边MN交于点E,F(如图2所示),设△ABC平移的时间为t(s)(0<t<6).
,将这块直角三角板按如图所示位置摆放.等边△ABC的顶点B与点O重合,BC边落在OM上,点A恰好落在斜边MN上,将等边△ABC从图1的位置沿OM方向以每秒1个单位长度的速度平移,边AB,AC分别与斜边MN交于点E,F(如图2所示),设△ABC平移的时间为t(s)(0<t<6).
(1)等边△ABC的边长为 ;
(2)在运动过程中,当 时,MN垂直平分AB;
(3)当0<t<6时,求直角三角板OMN与等边△ABC重叠部分的面积S与时间t之间的函数关系式.
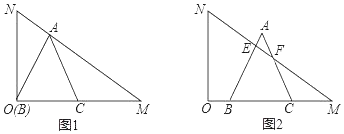
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,在等边△ABC中,点D为BC边上一动点,DE∥AB交AC于点E,将AD绕点D顺时针旋转60°得到DF,连接CF.则AE与FC的数量关系是 ;∠ACF的度数为 .

(2)拓展探究:如图2,在Rt△ABC中,∠ABC=90°,∠ACB=60°,点D为BC边上一动点,DE∥AB交AC于点E,当∠ADF=∠ACF=90°时,求![]() 的值.
的值.
(3)解决问题:如图3,在△ABC中,BC:AB=m,点D为BC的延长线上一点过点D作DE∥AB交AC的延长线于点E,直接写出当∠ADF=∠ACF=∠ABC时,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处![]() 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
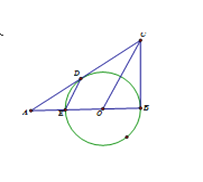
【题目】如图,Rt△ABC中,∠B=90°,O是AB上的一点,以O为圆心,OB为半径的圆与AB交于点E,交AC于点D,其中DE∥OC
(1)求证:AC为⊙O的切线;
(2)若AD=![]() ,且AB、AE的长是关于x的方程x2-4x+k=0的两个实数根,求⊙O的半径、CD的长.
,且AB、AE的长是关于x的方程x2-4x+k=0的两个实数根,求⊙O的半径、CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若三个非零实数x,y,z满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数x,y,z构成“和谐三组数”.
(1)实数1,2,3可以构成“和谐三组数”吗?请说明理由;
(2)若M(t,y1),N(t+1,y2),R(t+3,y3)三点均在函数y=![]() (k为常数,k≠0)的图象上,且这三点的纵坐标y1,y2,y3构成“和谐三组数”,求实数t的值;
(k为常数,k≠0)的图象上,且这三点的纵坐标y1,y2,y3构成“和谐三组数”,求实数t的值;
(3)若直线y=2bx+2c(bc≠0)与x轴交于点A(x1,0),与抛物线y=ax2+3bx+3c(a≠0)交于B(x2,y2),C(x3,y3)两点.
①求证:A,B,C三点的横坐标x1,x2,x3构成“和谐三组数”;
②若a>2b>3c,x2=1,求点P(![]() ,
,![]() )与原点O的距离OP的取值范围.
)与原点O的距离OP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作三角形的高线”的尺规作图过程.

已知:△ABC.
求作:BC边上的高线.
作法:如图,
①分别以A,B为圆心,大于![]() 长为半径画弧,两弧交于点D,E;
长为半径画弧,两弧交于点D,E;
②作直线DE,与AB交于点F,以点F为圆心,FA长为半径画圆,交CB的延长线于点G;
③连接AG.
所以线段AG就是所求作的BC边上的高线.

根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面证明.
证明:连接DA,DB,EA,EB,
∵DA=DB,
∴点D在线段AB的垂直平分线上( )(填推理的依据).
∵ = ,
∴点E在线段AB的垂直平分线上.
∴DE是线段AB的垂直平分线.
∴FA=FB.
∴AB是⊙F的直径.
∴∠AGB=90°( )(填推理的依据).
∴AG⊥BC
即AG就是BC边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌手机去年每台的售价y(元)与月份x之间满足函数关系:y=﹣50x+2600,去年的月销量p(万台)与月份x之间成一次函数关系,其中1﹣6月份的销售情况如下表:
月份(x) | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
销售量(p) | 3.9万台 | 4.0万台 | 4.1万台 | 4.2万台 | 4.3万台 | 4.4万台 |
(1)求p关于x的函数关系式;
(2)求该品牌手机在去年哪个月的销售金额最大?最大是多少万元?
(3)今年1月份该品牌手机的售价比去年12月份下降了m%,而销售量也比去年12月份下降了1.5m%.今年2月份,经销商决定对该手机以1月份价格的“八折”销售,这样2月份的销售量比今年1月份增加了1.5万台.若今年2月份这种品牌手机的销售额为6400万元,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com