
【题目】(1)问题发现:如图1,在等边△ABC中,点D为BC边上一动点,DE∥AB交AC于点E,将AD绕点D顺时针旋转60°得到DF,连接CF.则AE与FC的数量关系是 ;∠ACF的度数为 .

(2)拓展探究:如图2,在Rt△ABC中,∠ABC=90°,∠ACB=60°,点D为BC边上一动点,DE∥AB交AC于点E,当∠ADF=∠ACF=90°时,求![]() 的值.
的值.
(3)解决问题:如图3,在△ABC中,BC:AB=m,点D为BC的延长线上一点过点D作DE∥AB交AC的延长线于点E,直接写出当∠ADF=∠ACF=∠ABC时,![]() 的值.
的值.
【答案】(1)AE=CF,60°;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意可证△DEC是等边三角形,∠AED=120°,可得DE=DC,由旋转性质可得∠ADF=60°=∠EDC,AD=DF,由“SAS”可证△ADE≌△FDC,可得AE=CF,∠AED=∠DCF=120°,可得∠ACF=60°;
(2)通过证明△DAE∽△DFC,可得![]() ,通过证明△EDC∽△ABC,可得
,通过证明△EDC∽△ABC,可得![]() ,即可求
,即可求![]() 的值;
的值;
(3)通过证明△DAE∽△DFC,可得![]() ,通过证明△EDC∽△ABC,可得
,通过证明△EDC∽△ABC,可得![]() ,即可求
,即可求![]() 的值;
的值;
(1)∵DE∥AB
∴∠ABC=∠EDC=60°,∠BAC=∠DEC=60°
∴△DEC是等边三角形,∠AED=120°
∴DE=DC,
∵将AD绕点D顺时针旋转60°得到DF,
∴∠ADF=60°=∠EDC,AD=DF
∴∠ADE=∠FDC,且CD=DE,AD=DF
∴△ADE≌△FDC(SAS)
∴AE=CF,∠AED=∠DCF=120°
∴∠ACF=60°,
故答案为:AE=CF,60°
(2)∵∠ABC=90°,∠ACB=60°,
∴∠BAC=30°
∴tan∠BAC=![]()
∵DE∥AB
∴∠EDC=∠ABC=90°
∵∠ADF=90°,
∴∠ADE=∠FDC
∵∠ACF=90°,∠AED=∠EDC+∠ACB,∠FCD=∠ACF+∠ACB
∴∠AED=∠FCD,且∠ADE=∠FDC
∴△DAE∽△DFC
∴![]()
∵DE∥AB
∴△EDC∽△ABC
∴![]()
∴![]()
(3)∵AB∥DE
∴∠ABC=∠BDE=∠ADF,∠BAC=∠E
∴∠BDE+∠ADB=∠ADF+∠ADB
∴∠ADE=∠CDF,
∵∠ACD=∠ABC+∠BAC=∠ACF+∠DCF,且∠ACF=∠ABC
∴∠BAC=∠DCF=∠E,且∠ADE=∠CDF
∴△ADE∽△FDC
∴![]()
∵AB∥DE
∴△ABC∽△EDC
∴![]() ,且BC:AB=m,
,且BC:AB=m,
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC的直角顶点B在y轴上,边AB交x轴于点D(![]() ,0),点C的坐标为(﹣4,0),反比例函数y=
,0),点C的坐标为(﹣4,0),反比例函数y=![]() (k≠0)的图象过点A,则k=_____.
(k≠0)的图象过点A,则k=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
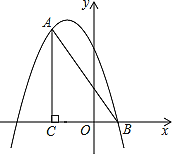
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块含30°角的直角三角板OMN,其中∠MON=90°,∠NMO=30°,ON=2![]() ,将这块直角三角板按如图所示位置摆放.等边△ABC的顶点B与点O重合,BC边落在OM上,点A恰好落在斜边MN上,将等边△ABC从图1的位置沿OM方向以每秒1个单位长度的速度平移,边AB,AC分别与斜边MN交于点E,F(如图2所示),设△ABC平移的时间为t(s)(0<t<6).
,将这块直角三角板按如图所示位置摆放.等边△ABC的顶点B与点O重合,BC边落在OM上,点A恰好落在斜边MN上,将等边△ABC从图1的位置沿OM方向以每秒1个单位长度的速度平移,边AB,AC分别与斜边MN交于点E,F(如图2所示),设△ABC平移的时间为t(s)(0<t<6).
(1)等边△ABC的边长为 ;
(2)在运动过程中,当 时,MN垂直平分AB;
(3)当0<t<6时,求直角三角板OMN与等边△ABC重叠部分的面积S与时间t之间的函数关系式.
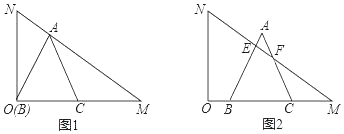
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组的同学测量一架无人飞机P的高度,如图,A,B两个观测点相距![]() ,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:
,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:![]() ,
,![]() ,sin71°≈0.95,tan71°≈2.90)
,sin71°≈0.95,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:

(1)①作出△ABC向左平移4个单位长度后得到的△A1B1C1, 并写出点C1的坐标;
②作出△ABC关于原点O对称的△A2B2C2, 并写出点C2的坐标;
(2)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论:①DF⊥AB;②CG=3GA;③CG=DF+GE;④S四边形BFGC=![]() 1中,说法正确的是( )
1中,说法正确的是( )

A. ①③④B. ②③C. ①③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发市场有中招考试文具套装,其中A品牌的批发价是每套20元,B品牌的批发价是每套25元,小王需购买A、B两种品牌的文具套装共1000套.
(1)若小王按需购买A、B两种品牌文具套装共用22000元,则各购买多少套?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000套文具套装,共用了y元,设A品牌文具套装买了x包,请求出y与x之间的函数关系式.
(3)若小王购买会员卡并用此卡按需购买1000套文具套装,共用了20000元,他计划在网店包邮销售这两种文具套装,每套文具套装小王需支付邮费8元,若A品牌每套销售价格比B品牌少5元,请你帮他计算,A品牌的文具套装每套定价不低于多少元时才不亏本(运算结果取整数)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).

(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com