
����Ŀ����һ�麬30���ǵ�ֱ�����ǰ�OMN�����С�MON��90������NMO��30����ON��2![]() �������ֱ�����ǰ尴��ͼ��ʾλ�ðڷţ��ȱ���ABC�Ķ���B���O�غϣ�BC������OM�ϣ���Aǡ������б��MN�ϣ����ȱ���ABC��ͼ1��λ����OM������ÿ��1����λ���ȵ��ٶ�ƽ�ƣ���AB��AC�ֱ���б��MN���ڵ�E��F����ͼ2��ʾ��������ABCƽ�Ƶ�ʱ��Ϊt��s����0��t��6����
�������ֱ�����ǰ尴��ͼ��ʾλ�ðڷţ��ȱ���ABC�Ķ���B���O�غϣ�BC������OM�ϣ���Aǡ������б��MN�ϣ����ȱ���ABC��ͼ1��λ����OM������ÿ��1����λ���ȵ��ٶ�ƽ�ƣ���AB��AC�ֱ���б��MN���ڵ�E��F����ͼ2��ʾ��������ABCƽ�Ƶ�ʱ��Ϊt��s����0��t��6����
��1���ȱ���ABC�ı߳�Ϊ�� ����
��2�����˶������У����� ��ʱ��MN��ֱƽ��AB��
��3����0��t��6ʱ����ֱ�����ǰ�OMN��ȱ���ABC�ص����ֵ����S��ʱ��t֮��ĺ�����ϵʽ��
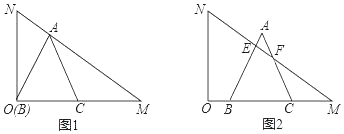
���𰸡���1��3����2��3����3�� .
.
��������
��1�����ݣ���OMN��30������ABCΪ�ȱ������Σ���֤��OAMΪֱ�������Σ�Ȼ�ɵó��𰸣�
��2����֪����C��M�غ�ʱֱ��MNƽ���߶�AB����ʱOB��3���ɴ˼��ɽ�����⣻
��3�����������ηֱ���⣺��0��t��3ʱ����CD��FM��D������S��S��MEB��2S��MDC�����㼴�ɣ��ڵ�3��t��6ʱ��S��S��MEB��
�⣺��1����Rt��MON�У��ߡ�MON��90����ON��2![]() ����M��30��
����M��30��
��OM��![]() ON��6��
ON��6��
�ߡ�ABCΪ�ȱ�������
���AOC��60����
���OAM��90��
��OA��MN������OAMΪֱ�������Σ�
��OA��![]() OM��
OM��![]() ��6��3��
��6��3��
�ʴ�Ϊ3��
��2����֪����C��M�غ�ʱֱ��MNƽ���߶�AB����ʱOB��3������t��3��
�ʴ�Ϊ3��
��3����֪��OM��6��MN��4![]() ��S��OMN��
��S��OMN��![]() ��2
��2![]() ��6��6
��6��6![]() ��
��
�ߡ�M��30������MBA��60����
���BEM��90����
�ٵ�0��t��3ʱ����CD��FM��D��

�ߡ�ACB��60������M��30������FCB����M+��CFM��
���CFM����M��30����
��CF��CM��
��CD��FM��
��DF��DM��
��S��CMF��2S��CDM��
�ߡ�MEB�ס�MON��
�� ��
��
��S��MEB��![]() ��
��
�ߡ�MDC�ס�MON��
�� ��
��
��S��MDC��![]() ��
��![]()
��S��S��MEB��2S��MDC����![]() ��
��
�ڵ�3��t��6ʱ��S��S��MEB��![]() ��
��
����������S�� ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ӡ�����ӽ���������������ܵ����㷺��ע��ijУ�͡��л��Ļ��Ҵ��Щ����ط�Ϸ����У����ϲ�����������������飬���ռ�����Ϣ����ͳ�ƣ���������������ͳ��ͼ��
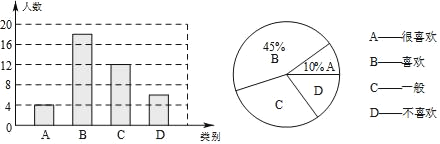
�������ͳ��ͼ���ṩ����Ϣ����������⣺
(1)���ε����������Ϊ�� ��������ͳ��ͼ��C���������ε�Բ�ĽǶ���Ϊ�� ����
(2)����У����ѧ��1200�ˣ���������������������Ƹ�Уѧ��ѡ��D��Ĵ�Լ�ж����ˣ�
(3)�ڵ����A��4���У��պ���2������2��Ů�������������ȡ����ͬѧ����������ɫ���û�����ͼ���б��ķ�������鵽������ѧ���Ա���ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���֪��A����3��0����B��0��4�����ԡ�OAB��������ת�任�����εõ���1����2����3����4���������2019��ֱ�Ƕ��������Ϊ��������

A. ��8076��0��B. ��8064��0��C. ��8076��![]() ��D. ��8064��
��D. ��8064��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��B�Ƿ���������y��![]() ��k��0��x��0��ͼ���ϵ����㣬BC��x�ᣬ��y���ڵ�C������P������ԭ��O��������O��A��B��C��ͼ����������ʾ·�ߣ������˶����յ�ΪC����P��PM��x�ᣬ����ΪM����������OMP�����ΪS��P���˶�ʱ��Ϊr����S����t�ĺ���ͼ�����Ϊ��������
��k��0��x��0��ͼ���ϵ����㣬BC��x�ᣬ��y���ڵ�C������P������ԭ��O��������O��A��B��C��ͼ����������ʾ·�ߣ������˶����յ�ΪC����P��PM��x�ᣬ����ΪM����������OMP�����ΪS��P���˶�ʱ��Ϊr����S����t�ĺ���ͼ�����Ϊ��������

A. 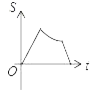 B.
B. 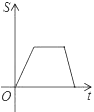 C.
C. 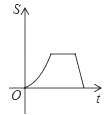 D.
D. 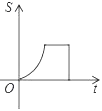
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�麬30���ǵ�ֱ�����ǰ�OMN�����С�MON��90������NMO��30����ON��2![]() �������ֱ�����ǰ尴��ͼ��ʾλ�ðڷţ��ȱ���ABC�Ķ���B���O�غϣ�BC������OM�ϣ���Aǡ������б��MN�ϣ����ȱ���ABC��ͼ1��λ����OM������ÿ��1����λ���ȵ��ٶ�ƽ�ƣ���AB��AC�ֱ���б��MN���ڵ�E��F����ͼ2��ʾ��������ABCƽ�Ƶ�ʱ��Ϊt��s����0��t��6����
�������ֱ�����ǰ尴��ͼ��ʾλ�ðڷţ��ȱ���ABC�Ķ���B���O�غϣ�BC������OM�ϣ���Aǡ������б��MN�ϣ����ȱ���ABC��ͼ1��λ����OM������ÿ��1����λ���ȵ��ٶ�ƽ�ƣ���AB��AC�ֱ���б��MN���ڵ�E��F����ͼ2��ʾ��������ABCƽ�Ƶ�ʱ��Ϊt��s����0��t��6����
��1���ȱ���ABC�ı߳�Ϊ�� ����
��2�����˶������У����� ��ʱ��MN��ֱƽ��AB��
��3����0��t��6ʱ����ֱ�����ǰ�OMN��ȱ���ABC�ص����ֵ����S��ʱ��t֮��ĺ�����ϵʽ��
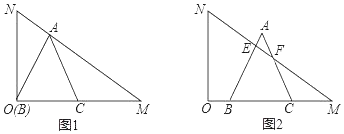
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ���Բ�����̳����˽������ij��ѧ�����ȡ�˲���ѧ�������ʾ����飬��������������![]() �dz��˽⣬
�dz��˽⣬![]() �˽⣬
�˽⣬![]() �˽���٣�
�˽���٣�![]() ���˽⣮������ֱ�ͳ�ƣ�����������������ͳ��ͼ(������)�������ͼ����Ϣ������������⣺
���˽⣮������ֱ�ͳ�ƣ�����������������ͳ��ͼ(������)�������ͼ����Ϣ������������⣺
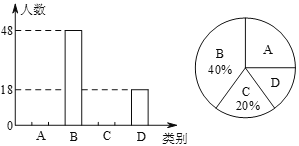
(1)�˴ι�������______��ѧ��������ͳ��ͼ��![]() ���ڵ����ε�Բ�ĽǶ���Ϊ______��
���ڵ����ε�Բ�ĽǶ���Ϊ______��
(2)������ͳ��ͼ����������
(3)����У����1600��ѧ����������ƶԲ�����̳����˽����Ϊ���dz��˽�����ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⷢ�֣���ͼ1���ڵȱ���ABC�У���DΪBC����һ���㣬DE��AB��AC�ڵ�E����AD�Ƶ�D˳ʱ����ת60���õ�DF������CF����AE��FC��������ϵ���� ������ACF�Ķ���Ϊ�� ����

��2����չ̽������ͼ2����Rt��ABC�У���ABC��90������ACB��60������DΪBC����һ���㣬DE��AB��AC�ڵ�E������ADF����ACF��90��ʱ����![]() ��ֵ��
��ֵ��
��3��������⣺��ͼ3������ABC�У�BC��AB��m����DΪBC���ӳ�����һ�����D��DE��AB��AC���ӳ����ڵ�E��ֱ��д������ADF����ACF����ABCʱ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
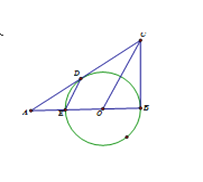
����Ŀ����ͼ,Rt��ABC��,��B��90��,O��AB�ϵ�һ��,��OΪԲ��,OBΪ�뾶��Բ��AB���ڵ�E,��AC�ڵ�D,����DE��OC
��1����֤��ACΪ��O�����ߣ�
��2����AD��![]() ,��AB��AE�ij��ǹ���x�ķ���x2��4x��k��0������ʵ����,���O�İ뾶��CD�ij�.
,��AB��AE�ij��ǹ���x�ķ���x2��4x��k��0������ʵ����,���O�İ뾶��CD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�4��������ABCD�У�E�DZ�BC���е㣬����CDE��ֱ��DE�۵���C���ڵ�F����Ƚ�����չƽ�����ۺ�DE������CF��BF��EF���ӳ�BF��AD�ڵ�G�������н��ۣ���BG= DE����CF��BG����sin��DFG= ![]() ����S��DFG=
����S��DFG=![]() ��������ȷ���У� ��
��������ȷ���У� ��

A. 1��
B. 2��
C. 3��
D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com