
【题目】若三个非零实数x,y,z满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数x,y,z构成“和谐三组数”.
(1)实数1,2,3可以构成“和谐三组数”吗?请说明理由;
(2)若M(t,y1),N(t+1,y2),R(t+3,y3)三点均在函数y=![]() (k为常数,k≠0)的图象上,且这三点的纵坐标y1,y2,y3构成“和谐三组数”,求实数t的值;
(k为常数,k≠0)的图象上,且这三点的纵坐标y1,y2,y3构成“和谐三组数”,求实数t的值;
(3)若直线y=2bx+2c(bc≠0)与x轴交于点A(x1,0),与抛物线y=ax2+3bx+3c(a≠0)交于B(x2,y2),C(x3,y3)两点.
①求证:A,B,C三点的横坐标x1,x2,x3构成“和谐三组数”;
②若a>2b>3c,x2=1,求点P(![]() ,
,![]() )与原点O的距离OP的取值范围.
)与原点O的距离OP的取值范围.
【答案】(1)不能,理由见解析;(2)t的值为﹣4、﹣2或2;(3)①证明见解析;②![]() ≤OP<
≤OP<![]() 且OP≠1.
且OP≠1.
【解析】
(1)由和谐三组数的定义进行验证即可;
(2)把M、N、R三点的坐标分别代入反比例函数解析式,可用t和k分别表示出y1、y2、y3,再由和谐三组数的定义可得到关于t的方程,可求得t的值;
(3)①由直线解析式可求得x1=﹣![]() ,联立直线和抛物线解析式消去y,利用一元二次方程根与系数的关系可求得x2+x3=﹣
,联立直线和抛物线解析式消去y,利用一元二次方程根与系数的关系可求得x2+x3=﹣![]() ,x2x3=
,x2x3=![]() ,再利用和谐三数组的定义证明即可;②由条件可得到a+b+c=0,可得c=﹣(a+b),由a>2b>3c可求得
,再利用和谐三数组的定义证明即可;②由条件可得到a+b+c=0,可得c=﹣(a+b),由a>2b>3c可求得![]() 的取值范围,令m=
的取值范围,令m=![]() ,利用两点间距离公式可得到OP2关于m的二次函数,利用二次函数的性质可求得OP2的取值范围,从而可求得OP的取值范围.
,利用两点间距离公式可得到OP2关于m的二次函数,利用二次函数的性质可求得OP2的取值范围,从而可求得OP的取值范围.
(1)不能,理由如下:
∵1、2、3的倒数分别为1、![]() 、
、![]() ,
,
∴![]() +
+![]() ≠1,1+
≠1,1+![]() ≠
≠![]() ,1+
,1+![]() ≠
≠![]() ,
,
∴实数1,2,3不可以构成“和谐三组数”;
(2)∵M(t,y1),N(t+1,y2),R(t+3,y3)三点均在函数![]() (k为常数,k≠0)的图象上,
(k为常数,k≠0)的图象上,
∴y1、y2、y3均不为0,且y1=![]() ,y2=
,y2=![]() ,y3=
,y3=![]() ,
,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,
,
∵y1,y2,y3构成“和谐三组数”,
∴有以下三种情况:
当![]() =
=![]() +
+![]() 时,则
时,则![]() =
=![]() +
+![]() ,即t=t+1+t+3,解得t=﹣4;
,即t=t+1+t+3,解得t=﹣4;
当![]() =
=![]() +
+![]() 时,则
时,则![]() =
=![]() +
+![]() ,即t+1=t+t+3,解得t=﹣2;
,即t+1=t+t+3,解得t=﹣2;
当![]() =
=![]() +
+![]() 时,则
时,则![]() =
=![]() +
+![]() ,即t+3=t+t+1,解得t=2;
,即t+3=t+t+1,解得t=2;
∴t的值为﹣4、﹣2或2;
(3)①∵a、b、c均不为0,
∴x1,x2,x3都不为0,
∵直线y=2bx+2c(bc≠0)与x轴交于点A(x1,0),
∴0=2bx1+2c,解得x1=﹣![]() ,
,
联立直线与抛物线解析式,消去y可得2bx+2c=ax2+3bx+3c,即ax2+bx+c=0,
∵直线与抛物线交与B(x2,y2),C(x3,y3)两点,
∴x2、x3是方程ax2+bx+c=0的两根,
∴x2+x3=﹣![]() ,x2x3=
,x2x3=![]() ,
,
∴![]() +
+![]() =
=![]() =
=![]() =﹣
=﹣![]() =
=![]() ,
,
∴x1,x2,x3构成“和谐三组数”;
②∵x2=1,
∴a+b+c=0,
∴c=﹣a﹣b,
∵a>2b>3c,
∴a>2b>3(﹣a﹣b),且a>0,整理可得![]() ,解得﹣
,解得﹣![]() <
<![]() <
<![]() ,
,
∵P(![]() ,
,![]() ),
),
∴OP2=(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2+(
)2+(![]() )2=2(
)2=2(![]() )2+2
)2+2![]() +1=2(
+1=2(![]() +
+![]() )2+
)2+![]() ,
,
令m=![]() ,则﹣
,则﹣![]() <m<
<m<![]() 且m≠0,且OP2=2(m+
且m≠0,且OP2=2(m+![]() )2+
)2+![]() ,
,
∵2>0,
∴当﹣![]() <m<﹣
<m<﹣![]() 时,OP2随m的增大而减小,当m=﹣
时,OP2随m的增大而减小,当m=﹣![]() 时,OP2有最大临界值
时,OP2有最大临界值![]() ,当m=﹣
,当m=﹣![]() 时,OP2有最小临界值
时,OP2有最小临界值![]() ,
,
当﹣![]() <m<
<m<![]() 时,OP2随m的增大而增大,当m=﹣
时,OP2随m的增大而增大,当m=﹣![]() 时,OP2有最小临界值
时,OP2有最小临界值![]() ,当m=
,当m=![]() 时,OP2有最大临界值
时,OP2有最大临界值![]() ,
,
∴![]() ≤OP2<
≤OP2<![]() 且OP2≠1,
且OP2≠1,
∵P到原点的距离为非负数,
∴![]() ≤OP<
≤OP<![]() 且OP≠1.
且OP≠1.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】大众服装店今年4月用4000元购进了一款衬衣若干件,上市后很快售完,服装店于5月初又购进该款衬衣,进货量比第一批增加了20%,由于第二批衬衣进货时价格比第一批衬衣进货时价格提高了20元,结果第二批衬衣进货用了6000元
(1)第一批衬衣进货时价格是多少?
(2)第一批衬衣售价为120元/件,为保证第二批衬衣的利润率不低于第一批衬衣的利润率,那么第二批衬衣每件售价至少是多少元?(提示:利润=售价﹣成本,利润率=利润÷成本×100%)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组的同学测量一架无人飞机P的高度,如图,A,B两个观测点相距![]() ,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:
,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:![]() ,
,![]() ,sin71°≈0.95,tan71°≈2.90)
,sin71°≈0.95,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论:①DF⊥AB;②CG=3GA;③CG=DF+GE;④S四边形BFGC=![]() 1中,说法正确的是( )
1中,说法正确的是( )

A. ①③④B. ②③C. ①③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发市场有中招考试文具套装,其中A品牌的批发价是每套20元,B品牌的批发价是每套25元,小王需购买A、B两种品牌的文具套装共1000套.
(1)若小王按需购买A、B两种品牌文具套装共用22000元,则各购买多少套?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000套文具套装,共用了y元,设A品牌文具套装买了x包,请求出y与x之间的函数关系式.
(3)若小王购买会员卡并用此卡按需购买1000套文具套装,共用了20000元,他计划在网店包邮销售这两种文具套装,每套文具套装小王需支付邮费8元,若A品牌每套销售价格比B品牌少5元,请你帮他计算,A品牌的文具套装每套定价不低于多少元时才不亏本(运算结果取整数)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,王老师让同学们对给定的正方形ABCD,如图.建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
甲同学:A(0,1),B(0,0),C(1,0),D(1,1);
乙同学:A(0,0),B(0,-1),C(1,-1),D(1,0);
丙同学:A(1,0),B(1,-2),C(3,-2),D(3,0);
丁同学:A(-1,2),B(-1,0),C(0,0),D(0,2);
上述四名同学表示的结果中,四个点的坐标都表示正确的同学是( )

A. 甲、乙、丙B. 乙、丙、丁C. 甲、丙D. 甲、乙、丙、丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC中,AB=BC=8,∠ABC=120°,BE是∠ABC的平分线,交AC于E,点D是AB的中点,连接DE,作EF∥AB于点F.
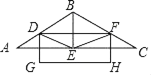
(1)求证四边形BDEF是菱形;
(2)如图以DF为一边作矩形DFHG,且点E是此矩形的对称中心,求矩形另一边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
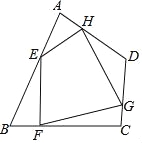
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com