
【题目】等腰△ABC中,AB=BC=8,∠ABC=120°,BE是∠ABC的平分线,交AC于E,点D是AB的中点,连接DE,作EF∥AB于点F.
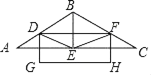
(1)求证四边形BDEF是菱形;
(2)如图以DF为一边作矩形DFHG,且点E是此矩形的对称中心,求矩形另一边的长.
【答案】(1)见解析;(2)FH=4.
【解析】
(1)先证明四边形BDEF是平行四边形,再根据DE=![]() AB=BD,即可得到四边形BDEF是菱形;
AB=BD,即可得到四边形BDEF是菱形;
(2)先证明四边形BEFH是平行四边形,得到BE=FH,再根据BE=![]() BC=4,即可得到FH=4.
BC=4,即可得到FH=4.
解:(1)∵AB=BC,BE是∠ABC的平分线,
∴E是AC的中点,且BE⊥AC,
又∵点D是AB的中点,
∴DE是△ABC的中位线,
∴DE∥BF,
又∵EF∥BD,
∴四边形BDEF是平行四边形,
又∵Rt△ABE中,点D是AB的中点,
∴DE=![]() AB=BD,
AB=BD,
∴四边形BDEF是菱形;
(2)连接EH,
∵点E是此矩形的对称中心,
∴D,E,H在同一直线上,
∵DE∥BF,
∴EH∥BF,
∵AB=BC,BE是∠ABC的角平分线,
∴点E是AC的中点,且BE⊥AC,
∵EF∥AB,
∴点F是BC的中点,
∵点D是AB的中点,
∴DF∥AC,
∴BE⊥DF,
又∵DFHG是矩形,
∴FH⊥DF,
∴BE∥FH,
∴四边形BEHF是平行四边形,
∴BE=FH,
∵∠ABC=120°,BE平分∠ABC,
∴∠EBF=60°,
又∵∠BEC=90°,
∴∠C=30°,
∴BE=![]() BC=4,
BC=4,
∴FH=4.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
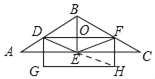
【题目】有一块含30°角的直角三角板OMN,其中∠MON=90°,∠NMO=30°,ON=2![]() ,将这块直角三角板按如图所示位置摆放.等边△ABC的顶点B与点O重合,BC边落在OM上,点A恰好落在斜边MN上,将等边△ABC从图1的位置沿OM方向以每秒1个单位长度的速度平移,边AB,AC分别与斜边MN交于点E,F(如图2所示),设△ABC平移的时间为t(s)(0<t<6).
,将这块直角三角板按如图所示位置摆放.等边△ABC的顶点B与点O重合,BC边落在OM上,点A恰好落在斜边MN上,将等边△ABC从图1的位置沿OM方向以每秒1个单位长度的速度平移,边AB,AC分别与斜边MN交于点E,F(如图2所示),设△ABC平移的时间为t(s)(0<t<6).
(1)等边△ABC的边长为 ;
(2)在运动过程中,当 时,MN垂直平分AB;
(3)当0<t<6时,求直角三角板OMN与等边△ABC重叠部分的面积S与时间t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若三个非零实数x,y,z满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数x,y,z构成“和谐三组数”.
(1)实数1,2,3可以构成“和谐三组数”吗?请说明理由;
(2)若M(t,y1),N(t+1,y2),R(t+3,y3)三点均在函数y=![]() (k为常数,k≠0)的图象上,且这三点的纵坐标y1,y2,y3构成“和谐三组数”,求实数t的值;
(k为常数,k≠0)的图象上,且这三点的纵坐标y1,y2,y3构成“和谐三组数”,求实数t的值;
(3)若直线y=2bx+2c(bc≠0)与x轴交于点A(x1,0),与抛物线y=ax2+3bx+3c(a≠0)交于B(x2,y2),C(x3,y3)两点.
①求证:A,B,C三点的横坐标x1,x2,x3构成“和谐三组数”;
②若a>2b>3c,x2=1,求点P(![]() ,
,![]() )与原点O的距离OP的取值范围.
)与原点O的距离OP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作三角形的高线”的尺规作图过程.

已知:△ABC.
求作:BC边上的高线.
作法:如图,
①分别以A,B为圆心,大于![]() 长为半径画弧,两弧交于点D,E;
长为半径画弧,两弧交于点D,E;
②作直线DE,与AB交于点F,以点F为圆心,FA长为半径画圆,交CB的延长线于点G;
③连接AG.
所以线段AG就是所求作的BC边上的高线.

根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面证明.
证明:连接DA,DB,EA,EB,
∵DA=DB,
∴点D在线段AB的垂直平分线上( )(填推理的依据).
∵ = ,
∴点E在线段AB的垂直平分线上.
∴DE是线段AB的垂直平分线.
∴FA=FB.
∴AB是⊙F的直径.
∴∠AGB=90°( )(填推理的依据).
∴AG⊥BC
即AG就是BC边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC的内心,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+![]() ∠A;②EF不可能是△ABC的中位线;③设OD=m,AE+AF=n,则S△AEF=
∠A;②EF不可能是△ABC的中位线;③设OD=m,AE+AF=n,则S△AEF=![]() mn;④以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切.其中正确结论的个数是( )
mn;④以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切.其中正确结论的个数是( )
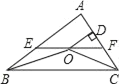
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长4的正方形ABCD中,E是边BC的中点,将△CDE沿直线DE折叠后,点C落在点F处,冉将其打开、展平,得折痕DE。连接CF、BF、EF,延长BF交AD于点G。则下列结论:①BG= DE;②CF⊥BG;③sin∠DFG= ![]() ;④S△DFG=
;④S△DFG=![]() .其中正确的有( )
.其中正确的有( )

A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器超出5个的部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x(x>5)个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
(3)当需要购买50个计算器时,买哪种品牌的计算器更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌手机去年每台的售价y(元)与月份x之间满足函数关系:y=﹣50x+2600,去年的月销量p(万台)与月份x之间成一次函数关系,其中1﹣6月份的销售情况如下表:
月份(x) | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
销售量(p) | 3.9万台 | 4.0万台 | 4.1万台 | 4.2万台 | 4.3万台 | 4.4万台 |
(1)求p关于x的函数关系式;
(2)求该品牌手机在去年哪个月的销售金额最大?最大是多少万元?
(3)今年1月份该品牌手机的售价比去年12月份下降了m%,而销售量也比去年12月份下降了1.5m%.今年2月份,经销商决定对该手机以1月份价格的“八折”销售,这样2月份的销售量比今年1月份增加了1.5万台.若今年2月份这种品牌手机的销售额为6400万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线系数”.
(1)任意抛物线都有“抛物线三角形”是______(填“真”或“假”)命题;
(2)若一条抛物线系数为[1,0,-2],则其“抛物线三角形”的面积为________;
(3)若一条抛物线系数为[-1,2b,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式;
(4)在(3)的前提下,该抛物线的顶点为A,与x轴交于O,B两点,在抛物线上是否存在一点P,过P作PQ⊥x轴于点Q,使得△BPQ∽△OAB,如果存在,求出P点坐标,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com