
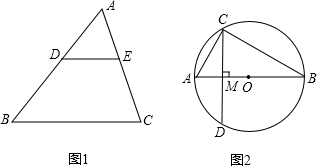
 (1)如图1在△ABC中,D为AB上一点,DE∥BC交AC于点E,若AD:DB=2:3,BC=10,求DE的长.
(1)如图1在△ABC中,D为AB上一点,DE∥BC交AC于点E,若AD:DB=2:3,BC=10,求DE的长.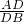 =
= ,
, =
= ,
, =
= =
= ,
, AB=1,
AB=1, =
= ,
, ×AB×CM=
×AB×CM= ×AC×BC,
×AC×BC, ,
, ,
, =
= ,
, .
. =
= =
= ,代入求出即可.
,代入求出即可.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com