
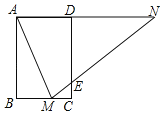
【题目】如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E.
(1)求证:△AMN是等腰三角形;
(2)求证:AM2=2BMAN;
(3)当M为BC中点时,求ME的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)利用矩形和平行线的性质求证∠AMN=∠NAM,从而等角对等边;(2)根据等腰三角形和相似三角形的性质列比例式,得到ANBM=AHAM=![]() AM2,从而求证;(3)由(2)的结论和已知条件求得AN=5,DN=3,然后根据平行线判定△DNE∽△CME,从而列出比例式求DE的长度,最后利用勾股定理求解.
AM2,从而求证;(3)由(2)的结论和已知条件求得AN=5,DN=3,然后根据平行线判定△DNE∽△CME,从而列出比例式求DE的长度,最后利用勾股定理求解.
(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠NAM=∠BMA,
∵∠AMN=∠AMB,
∴∠AMN=∠NAM,
∴AN=MN,即△AMN是等腰三角形;
(2)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=2,AB=CD=3,
∴∠NAM=∠BMA,
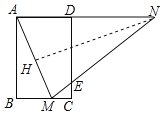
作NH⊥AM于H,如图所示:
∵AN=MN,NH⊥AM,
∴AH=![]() AM,
AM,
∵∠NHA=∠ABM=90°,∠NAM=∠BMA,
∴△NAH∽△AMB,
∴![]() ,
,
∴ANBM=AHAM=![]() AM2,
AM2,
∴AM2=2BMAN;
(3)∵M为BC中点,
∴BM=CM=![]() BC=
BC=![]() ×2=1,
×2=1,
由(2)得:AM2=2BMAN,
即:AM2=2AN,
∵AM2=AB2+BM2=32+12=10,
∴10=2AN,
∴AN=5,
∴DN=AN﹣AD=5﹣2=3,
设DE=x,则CE=3﹣x,
∵AN∥BC,
∴△DNE∽△CME
∴![]() ,即
,即![]() ,
,
解得:x=![]() ,即DE=
,即DE=![]() ,
,
∴CE=DC﹣DE=3﹣![]() =
=![]() ,
,
∴在Rt△MEC中,ME=![]() .
.


科目:初中数学 来源: 题型:
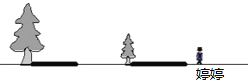
【题目】两棵树(大树和小树)在一盏路灯下的影子如图所示
(1)确定路灯灯泡的位置(用点P表示)和表示婷婷的影长的线段(用线段AB表示).
(2)若小树高为2m,影长为4m;婷婷高1.5m,影长为4.5米,且婷婷距离小树10米,试求出路灯灯泡的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
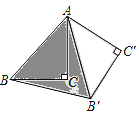
【题目】如图,在△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A逆时针方向旋转60°到△AB'C'的位置,则图中阴影部分的面积是( )
,将△ABC绕点A逆时针方向旋转60°到△AB'C'的位置,则图中阴影部分的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
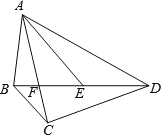
【题目】如图,四边形ABCD的对角线AC,BD交于点F,点E是BD上一点,且∠BAC=∠BDC=∠DAE.
(1)求证:△ABE∽△ACD;
(2)若BC=2,AD=6,DE=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
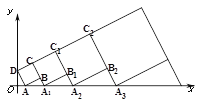
【题目】在平面直角坐标系![]() 中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为____________;第n个正方形的面积为____________.
中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第1个正方形的面积为____________;第n个正方形的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
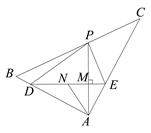
【题目】△ABC中,AB=6,AC=8,BC=10,P为BC边上一动点,过线段AP上的点M作DE⊥AP,交边AB于点D,交边AC于点E,点N为DE中点,若四边形ADPE的面积为18,则AN的最大值=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某幢大楼顶部有广告牌CD,小宇身高MA为1.89米,他站在立在离大楼45米的A处测得大楼顶端点D的仰角为30°;接着他向大楼前进15米,站在点B处测得广告牌顶端点C的仰角为45°.
(1)求这幢大楼的高DH;
(2)求这块广告牌CD的高度.(取![]() ≈1.732,计算结果保留一位小数)
≈1.732,计算结果保留一位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
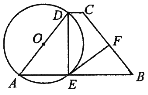
【题目】梯形ABCD中,AB∥DC,AD=BC,以AD为直径的⊙O交AB于E,⊙O的切线EF交BC于F,求证:
(1)EF⊥BC; (2)BF·BC=BE·AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用恰当的方法解下列方程.
(1)3(2x+1)2=27
(2)2x2﹣3x﹣1=0
(3)3(x﹣1)2=2(x﹣1)
(4)x2﹣(2x+1)2=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com