
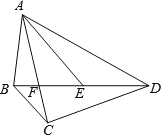
【题目】如图,四边形ABCD的对角线AC,BD交于点F,点E是BD上一点,且∠BAC=∠BDC=∠DAE.
(1)求证:△ABE∽△ACD;
(2)若BC=2,AD=6,DE=3,求AC的长.
【答案】(1)见解析 (2)AC=4
【解析】
试题(1)根据∠BAC=∠DAE得到∠BAE=∠CAD,根据∠BAC=∠BDC,∠BFA=∠CFD得到∠ABE=∠ACD,从而说明△ABE和△ACD相似;(2)根据△ABE∽△ACD得到![]() =
=![]() ,再根据∠BAC=∠DAE得到△ABC和△AED相似,根据相似比求出AC的值.
,再根据∠BAC=∠DAE得到△ABC和△AED相似,根据相似比求出AC的值.
试题解析:(1)∵∠BAC=∠DAE,∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD.
又∵∠BAC=∠BDC,∠BFA=∠CFD, ∴180°-∠BAC-∠BFA=180°-∠BDC-∠CFD,即∠ABE=∠ACD.
∴△ABE∽△ACD.
(2)∵△ABE∽△ACD,∴![]() =
=![]() . 又∵∠BAC=∠DAE, ∴△ABC∽△AED,
. 又∵∠BAC=∠DAE, ∴△ABC∽△AED,
∴![]() =
=![]() , ∴AC=
, ∴AC=![]() =
=![]() =4.
=4.


科目:初中数学 来源: 题型:
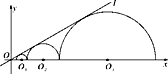
【题目】如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线l相切.设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当直线l与x轴所成锐角为30°,且r1=1时,r2018=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点A在y轴正半轴上,顶点C在x轴正半轴上,抛物线![]() (a<0)的顶点为D,且经过点A、B.若△ABD为等腰直角三角形,则a的值为___________.
(a<0)的顶点为D,且经过点A、B.若△ABD为等腰直角三角形,则a的值为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水库上游有一单孔抛物线型拱桥,它的跨度AB为100米.最低水位(与AB在同一平面)时桥面CD距离水面25米,桥拱两端有两根25米高的水泥柱BC和AD,中间等距离竖立9根钢柱支撑桥面,拱顶正上方的钢柱EF长5米.
(1)建立适当的直角坐标系,求抛物线型桥拱的解析式;
(2)在最低水位时,能并排通过两艘宽28米,高16米的游轮吗?(假设两游轮之间的安全间距为4米)
(3)由于下游水库蓄水及雨季影响导致水位上涨,水位最高时比最低水位高出13米,请问最高水位时没在水面以下的钢柱总长为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别在BC、AB、CA上,且DE∥CA,DF∥BA,则下列三种说法:
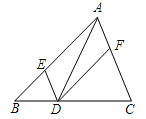
(1)如果∠BAC=90°,那么四边形AEDF是矩形
(2)如果AD平分∠BAC,那么四边形AEDF是菱形
(3)如果AD⊥BC且AB=AC,那么四边形AEDF是正方形 .其中正确的有 ( )
A.3个 B.2个 C.1个 D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( ).
A. 一个游戏的中奖概率是![]() ,则做10次这样的游戏一定会中奖
,则做10次这样的游戏一定会中奖
B. 一组数据6,8,7,8,8,9,10的众数和中位数都是8
C. 为了解全国中学生的心理健康情况,应该采用普查的方式
D. 若甲组数据的方差S2甲=0.01,乙组数据的方差S2乙=0.1,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
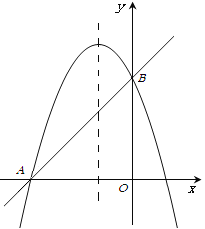
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,已知经过点
,已知经过点![]() 的直线的表达式为
的直线的表达式为![]() .
.
(1)求抛物线的函数表达式及其顶点![]() 的坐标;
的坐标;
(2)如图①,点![]() 是线段
是线段![]() 上的一个动点,其中
上的一个动点,其中![]() ,作直线
,作直线![]() 轴,交直线
轴,交直线![]() 于
于![]() ,交抛物线于
,交抛物线于![]() ,作
,作![]() ∥
∥![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,四边形
,四边形![]() 为矩形.设矩形
为矩形.设矩形![]() 的周长为
的周长为![]() ,写出
,写出![]() 与
与![]() 的函数关系式,并求
的函数关系式,并求![]() 为何值时周长
为何值时周长![]() 最大;
最大;
(3)如图②,在抛物线的对称轴上是否存在点![]() ,使点
,使点![]() 构成的三角形是以
构成的三角形是以![]() 为腰的等腰三角形.若存在,直接写出所有符合条件的点
为腰的等腰三角形.若存在,直接写出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
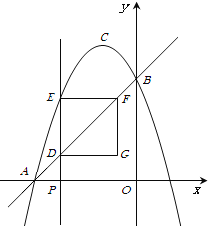
图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进价为8元的商品按每件10元出售,每天可销售200件,现商家采用提高售价,减少进货量的方法增加利润,如果这种商品每件涨0.5元,其销量就会减少10件,那么要使利润为640元,需将售价定为( )
A. 16元 B. 12元 C. 16元或12元 D. 14元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,已知⊙O的直径为AB,AC⊥AB于点A, BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.下面四个结论:①ED是⊙O的切线;②BC=2OE③△BOD为等边三角形;④△EOD ∽ △CAD,正确的是( )

A. ①② B. ②④ C. ①②④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com