
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌвбжЊОЙ§Еу
ЃЌвбжЊОЙ§Еу![]() ЕФжБЯпЕФБэДяЪНЮЊ
ЕФжБЯпЕФБэДяЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНМАЦфЖЅЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМЂйЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФвЛИіЖЏЕуЃЌЦфжа
ЩЯЕФвЛИіЖЏЕуЃЌЦфжа![]() ЃЌзїжБЯп
ЃЌзїжБЯп![]() жсЃЌНЛжБЯп
жсЃЌНЛжБЯп![]() гк
гк![]() ЃЌНЛХзЮяЯпгк
ЃЌНЛХзЮяЯпгк![]() ЃЌзї
ЃЌзї![]() ЁЮ
ЁЮ![]() жсЃЌНЛжБЯп
жсЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЮЊОиаЮЃЎЩшОиаЮ
ЮЊОиаЮЃЎЩшОиаЮ![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЌаДГі
ЃЌаДГі![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓ
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓ![]() ЮЊКЮжЕЪБжмГЄ
ЮЊКЮжЕЪБжмГЄ![]() зюДѓЃЛ
зюДѓЃЛ
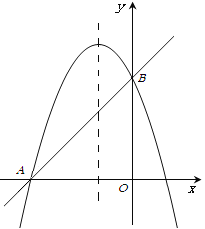
ЃЈ3ЃЉШчЭМЂкЃЌдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕу
ЃЌЪЙЕу![]() ЙЙГЩЕФШ§НЧаЮЪЧвд
ЙЙГЩЕФШ§НЧаЮЪЧвд![]() ЮЊбќЕФЕШбќШ§НЧаЮЃЎШєДцдкЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕу
ЮЊбќЕФЕШбќШ§НЧаЮЃЎШєДцдкЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЭМЂй ЭМЂк
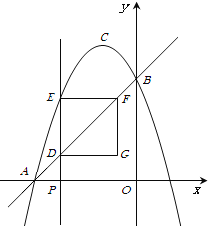
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпЕФБэДяЪНЮЊy=-x2-2x+3ЃЌЖЅЕуCзјБъЮЊЃЈ-1,4ЃЉЃЛ
ЃЈ2ЃЉL=-4m2-12m=-4ЃЈm+![]() ЃЉ2+9ЃЛ
ЃЉ2+9ЃЛ
ЕБm=-![]() ЪБЃЌзюДѓжЕL=9ЃЛ
ЪБЃЌзюДѓжЕL=9ЃЛ
ЃЈ3ЃЉЕуQЕФзјБъЮЊЃЈ-1ЃЌ![]() ЃЉЃЌЃЈ-1ЃЌ-
ЃЉЃЌЃЈ-1ЃЌ-![]() ЃЉЃЌЃЈ-1ЃЌ3+
ЃЉЃЌЃЈ-1ЃЌ3+![]() ЃЉЃЌЃЈ-1ЃЌ3-
ЃЉЃЌЃЈ-1ЃЌ3-![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉгЩжБЯпОЙ§AЁЂBСНЕуПЩЧѓЕУетСНЕуЕФзјБъЃЌШЛКѓДњШыЖўДЮКЏЪ§НтЮіЪНМДПЩЧѓГіbЁЂcЕФжЕЃЌДгЖјЕУЕННтЮіЪНЃЌНјЖјЕУЕНЖЅЕуЕФзјБъЃЛ
ЃЈ2ЃЉгЩЬтвтПЩБэЪОГіDЁЂEЕФзјБъЃЌДгЖјЕУЕНDEЕФГЄЃЌгЩвбжЊЬѕМўПЩЕУDE=EFЃЌДгЖјПЩБэЪОГіОиаЮDEFGЕФжмГЄLЃЌРћгУЖўДЮКЏЪ§ЕФаджЪПЩЧѓЕУзюДѓжЕЃЛ
ЃЈ3ЃЉЗжБ№вдЕуAЁЂЕуBЮЊдВаФЃЌвдABГЄЮЊАыОЖЛдВЃЌдВгыЖдГЦжсЕФНЛЕуМДЮЊЫљЧѓЕФЕуЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉжБЯпy=x+3гыxжсЯрНЛгкAЃЈ-3,0 ЃЉЃЌгыyжсЯрНЛгкBЃЈ0,3ЃЉ
ХзЮяЯпy=-x2+bx+cОЙ§AЃЈ-3,0 ЃЉЃЌBЃЈ0,3ЃЉЃЌЫљвдЃЌ
![]() ,
,
Ёр![]() ЃЌ
ЃЌ
ЫљвдХзЮяЯпЕФБэДяЪНЮЊy=-x2-2x+3ЃЌ
Ёпy=-x2-2x+3=-ЃЈx+1ЃЉ2+4,
ЫљвдЃЌЖЅЕузјБъЮЊCЃЈ-1,4ЃЉЃЎ
ЃЈ2ЃЉвђЮЊDдкжБЯпy=x+3ЩЯЃЌЁрDЃЈm,m+3ЃЉЃЎ
вђЮЊEдкХзЮяЯпЩЯЃЌЁрEЃЈmЃЌ-m2-2m+3ЃЉЃЎ
DE=-m2-2m+3-ЃЈm+3ЃЉ=-m2-3mЃЎ
гЩЬтвтПЩжЊЃЌAO=BO,
ЁрЁЯDAP=ЁЯADP=ЁЯEDF=ЁЯEFD=45ЁуЃЌ
ЁрDE=EFЃЎ
L=4DE=-4m2-12mЃЎ
L=-4m2-12m=-4ЃЈm+![]() ЃЉ2+9ЃЎ
ЃЉ2+9ЃЎ
Ёпa=-4<0,
ЁрЖўДЮКЏЪ§газюДѓжЕ
ЕБm=-![]() ЪБЃЌзюДѓжЕL=9ЃЎ
ЪБЃЌзюДѓжЕL=9ЃЎ
ЃЈ3ЃЉЕуQЕФзјБъЮЊЃЈ-1ЃЌ![]() ЃЉЃЌЃЈ-1ЃЌ-
ЃЉЃЌЃЈ-1ЃЌ-![]() ЃЉЃЌЃЈ-1ЃЌ3+
ЃЉЃЌЃЈ-1ЃЌ3+![]() ЃЉЃЌЃЈ-1ЃЌ3-
ЃЉЃЌЃЈ-1ЃЌ3-![]() ЃЉЃЎ
ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїгыаЁССЭцгЮЯЗЃЌШчЭМЃЌСНзщЯрЭЌЕФПЈЦЌЃЌУПзщШ§еХЃЌЕквЛзщПЈЦЌе§УцЗжБ№БъгаЪ§зж1ЃЌ3ЃЌ5ЃЛЕкЖўзщПЈЦЌе§УцЗжБ№БъгаЪ§зж2ЃЌ4ЃЌ6ЃЎЫћУЧНЋПЈЦЌБГУцГЏЩЯЃЌЗжзщГфЗжЯДдШКѓЃЌДгУПзщПЈЦЌжаИїУўГівЛеХЃЌГЦЮЊвЛДЮгЮЯЗЃЎЕБУўГіЕФСНеХПЈЦЌЕФе§УцЪ§зжжЎЛ§аЁгк10ЃЌдђаЁУїЛёЪЄЃЛЕБУўГіЕФСНеХПЈЦЌЕФе§УцЪ§зжжЎЛ§ГЌЙ§10ЃЌдђаЁССЛёЪЄЃЎФуШЯЮЊетИігЮЯЗЙцдђЖдЫЋЗНЙЋЦНТ№ЃПЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
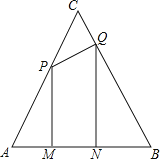
ЁОЬтФПЁПШчЭМЃЌЕШБпШ§НЧаЮABCЕФБпГЄЮЊ8cmЃЌЖЏЕуPДгЕуAГіЗЂвд![]() УыЕФЫйЖШбиACЗНЯђЯђжеЕуCдЫЖЏЃЌЭЌЪБЖЏЕуQДгЕуCГіЗЂвд
УыЕФЫйЖШбиACЗНЯђЯђжеЕуCдЫЖЏЃЌЭЌЪБЖЏЕуQДгЕуCГіЗЂвд![]() УыЕФЫйЖШбиCBЗНЯђЯђжеЕуBдЫЖЏЃЌЙ§ЕуPЁЂQЗжБ№зїБпABЕФДЙЯпЖЮPMЁЂQNЃЌДЙзуЗжБ№ЮЊЕуMЁЂ
УыЕФЫйЖШбиCBЗНЯђЯђжеЕуBдЫЖЏЃЌЙ§ЕуPЁЂQЗжБ№зїБпABЕФДЙЯпЖЮPMЁЂQNЃЌДЙзуЗжБ№ЮЊЕуMЁЂ![]() ЩшPЁЂQСНЕудЫЖЏЪБМфЮЊtУы
ЩшPЁЂQСНЕудЫЖЏЪБМфЮЊtУы![]() ЃЌЫФБпаЮMNQPЕФУцЛ§ЮЊ
ЃЌЫФБпаЮMNQPЕФУцЛ§ЮЊ![]() ЃЎ
ЃЎ
![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЮЊЕШБпШ§НЧаЮЃП
ЮЊЕШБпШ§НЧаЮЃП
![]() ЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЫФБпаЮMNQPЕФУцЛ§SЕШгк
ЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЫФБпаЮMNQPЕФУцЛ§SЕШгк![]() ЕФУцЛ§ЕФ
ЕФУцЛ§ЕФ![]() ЃПШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
![]() СЌНгPNЁЂQMНЛгкЕуDЃЌЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙ
СЌНгPNЁЂQMНЛгкЕуDЃЌЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙ![]() ЃПШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
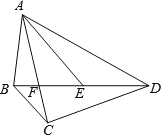
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЕФЖдНЧЯпACЃЌBDНЛгкЕуFЃЌЕуEЪЧBDЩЯвЛЕуЃЌЧвЁЯBACЃНЁЯBDCЃНЁЯDAEЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABEЁзЁїACDЃЛ
ЃЈ2ЃЉШєBCЃН2ЃЌADЃН6ЃЌDEЃН3ЃЌЧѓACЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯB=90ЁуЃЌAB=12ЃЌBC=24ЃЌЖЏЕуPДгЕуAПЊЪМбиБпABЯђжеЕуBвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШвЦЖЏЃЌЖЏЕуQДгЕуBПЊЪМбиБпBCвдУПУы4ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕуCвЦЖЏЃЌШчЙћЕуPЁЂQЗжБ№ДгЕуAЁЂBЭЌЪБГіЗЂЃЌФЧУДЁїPBQЕФУцЛ§SЫцГіЗЂЪБМфtЃЈsЃЉШчКЮБфЛЏЃПаДГіКЏЪ§ЙиЯЕЪНМАtЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌБпГЄЮЊ1ЕФе§ЗНаЮABCDЕФЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌжБНЧЁЯMPNЕФЖЅЕуPгыЕуOжиКЯЃЌжБНЧБпPMЃЌPNЗжБ№гыOAЃЌOBжиКЯЃЌШЛКѓФцЪБеыа§зЊЁЯMPNЃЌа§зЊНЧЮЊІШЃЈ0ЁуЃМІШЃМ90ЁуЃЉЃЌPMЁЂPNЗжБ№НЛABЁЂBCгкEЁЂFСНЕуЃЌСЌНгEFНЛOBгкЕуGЃЌдђЯТСаНсТлжае§ШЗЕФЪЧ_____.
ЃЈ1ЃЉEF=![]() OEЃЛЃЈ2ЃЉSЫФБпаЮOEBFЃКSе§ЗНаЮABCD=1ЃК4ЃЛЃЈ3ЃЉдка§зЊЙ§ГЬжаЃЌЕБЁїBEFгыЁїCOFЕФУцЛ§жЎКЭзюДѓЪБЃЌAE=
OEЃЛЃЈ2ЃЉSЫФБпаЮOEBFЃКSе§ЗНаЮABCD=1ЃК4ЃЛЃЈ3ЃЉдка§зЊЙ§ГЬжаЃЌЕБЁїBEFгыЁїCOFЕФУцЛ§жЎКЭзюДѓЪБЃЌAE=![]() ЃЛЃЈ4ЃЉOGBD=AE2+CF2.
ЃЛЃЈ4ЃЉOGBD=AE2+CF2.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃвЊЧѓ340УћбЇЩњНјааЩчЛсЕїВщЃЌУПШЫаыЭъГЩ3Љ6ЗнБЈИцЃЎЕїВщНсЪјКѓЫцЛњГщВщСЫ20УћбЇЩњУПШЫЭъГЩБЈИцЕФЗнЪ§ЃЌВЂЗжЮЊЫФРрЃЌAЃК3ЗнЃЛBЃК4ЗнЃЛCЃК5ЗнЃЛDЃК6ЗнЃЎНЋИїРрЕФШЫЪ§ЛцжЦГЩЩШаЮЭМЃЈШчЭМ1ЃЉКЭЬѕаЮЭМЃЈШчЭМ2ЃЉЃЌОШЗШЯЩШаЮЭМЪЧе§ШЗЕФЃЌЖјЬѕаЮЭМЩагавЛДІДэЮѓЃЎ
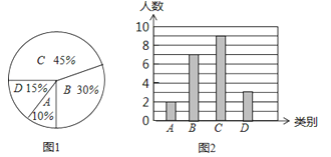
ЛиД№ЮЪЬтЃК
ЃЈ1ЃЉаДГіЬѕаЮЭМжаДцдкЕФДэЮѓЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉаДГіет20УћбЇЩњУПШЫЭъГЩБЈИцЗнЪ§ЕФжкЪ§ЁЂжаЮЛЪ§ЃЛ
ЃЈ3ЃЉдкЧѓет20УћбЇЩњУПШЫЭъГЩБЈИцЗнЪ§ЕФЦНОљЪ§ЪБЃЌаЁОВЪЧетбљЗжЮіЕФЃК
ЕквЛВНЧѓЦНОљЪ§ЕФЙЋЪНЪЧ![]() =
=![]() ЃЛ
ЃЛ
ЕкЖўВНдкИУЮЪЬтжаЃЌn=4ЃЌx1=3ЃЌx2=4ЃЌx3=5ЃЌx4=6ЃЛ
ЕкШ§ВНЃК![]() =
=![]() =4.5ЃЈЗнЃЉ
=4.5ЃЈЗнЃЉ
ЂйаЁОВЕФЗжЮіЪЧДгФФвЛВНПЊЪМГіЯжДэЮѓЕФЃП
ЂкЧыФуАяЫ§МЦЫуГіе§ШЗЕФЦНОљЪ§ЃЌВЂЙРМЦет340УћбЇЩњЙВЭъГЩБЈИцЖрЩйЗнЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
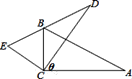
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌШєвдЕуCЮЊа§зЊжааФЃЌНЋ
ЃЌШєвдЕуCЮЊа§зЊжааФЃЌНЋ![]() а§зЊІШЕН
а§зЊІШЕН![]() ЕФЮЛжУЃЌЪЙЕуBЧЁКУТфдкБп
ЕФЮЛжУЃЌЪЙЕуBЧЁКУТфдкБп![]() ЩЯЃЌдђІШЕШгкЃЈ ЃЉ
ЩЯЃЌдђІШЕШгкЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
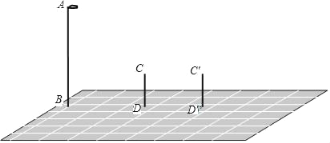
ЁОЬтФПЁПШчЭМЃЌABБэЪОТЗЕЦЃЌCDЁЂCЁфDЁфБэЪОаЁУїЫљдкСНИіВЛЭЌЮЛжУЃК
ЃЈ1ЃЉЗжБ№ЛГіетСНИіВЛЭЌЮЛжУаЁУїЕФгАзгЃЛ
ЃЈ2ЃЉаЁУїЗЂЯждкетСНИіВЛЭЌЕФЮЛжУЩЯЃЌЫћЕФгАзгГЄЗжБ№ЪЧздМКЩэИпЕФ1БЖКЭ2БЖЃЌЫћгжСПЕУздМКЕФЩэИпЮЊ1.5УзЃЌDDЁфГЄЮЊ3УзЃЌФуФмАяЫћЫуГіТЗЕЦЕФИпЖШТ№ЃПЃЈBЁЂDЁЂDЁфдквЛЬѕжБЯпЩЯЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com