
【题目】如图,顶点为(1,4)的抛物线 ![]() 与直线
与直线 ![]() 交于点A(2,2),直线
交于点A(2,2),直线 ![]() 与
与 ![]() 轴交于点B与
轴交于点B与 ![]() 轴交于点C.
轴交于点C.
(1)求 ![]() 的值及抛物线的解析式
的值及抛物线的解析式
(2)P为抛物线上的点,点P关于直线AB的对称轴点在 ![]() 轴上,求点P的坐标
轴上,求点P的坐标
(3)点D为 ![]() 轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
【答案】
(1)
解:将A(2,2)代入y=![]() x+n得n=1;
x+n得n=1;
设抛物线的解析式y=a![]() +4;
+4;
代入点A(2,2),可得a=-2;
所以抛物线的解析式y=-2![]() +4=-2
+4=-2![]() +4x+2;
+4x+2;
(2)
解:如图1.设PP′与AC的交点为H,作HM⊥x轴于M,作PN⊥HM于N
设P(x,-2![]() +4x+2),H(m,
+4x+2),H(m,![]() m+1)
m+1)
∵H是PP′的中点,
∴NM=2HM;
∴-2![]() +4x+2=m+2;
+4x+2=m+2;
∴m=-2![]() +4x ①;
+4x ①;
又∵![]() ,NH=HM;
,NH=HM;
∴HM=2PN;
∴![]() m+1=2(m-x),
m+1=2(m-x),
∴4x=3m-2 ②;
联立① ②解得x=1或x=![]() ,
,
∴点P的坐标(1,4)(如图2)或![]() (如图3)
(如图3)
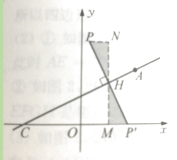
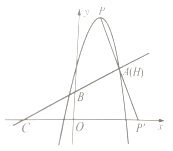
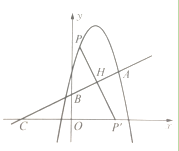
图1 图2 图3
(3)
解:设点E坐标为(t,0),以AB为边或对角线进行分类讨论:
①如图4,当AB是平行四边行的边时,AB//DE,AB=DE;
∵点B(0,1)先向右平移2个单位,再向上平移1个单位得到A(2,2),
∴D(t+2,1);
将D(t+2,1)代入y=-2![]() +4,得-2
+4,得-2![]() +4=1;
+4=1;
解得t=![]() 或t=
或t=![]() ,
,
∴E(![]() ,0)(如图6)或E(
,0)(如图6)或E(![]() ,0)(如图5)
,0)(如图5)
②如图7,当AB是平行四边形的对角线时,设AB的中点G(1,![]() ),点E(t,0);
),点E(t,0);
∴E关于G(1,![]() )的对称点D的坐标可以表示为(2-t,3)
)的对称点D的坐标可以表示为(2-t,3)
将D(2-t,3)代入y=-2![]() +4,得-2
+4,得-2![]() +4=3;
+4=3;
解得t=![]() 或t=
或t=![]() ,
,
∴E(![]() ,0)(如图9)或E(
,0)(如图9)或E(![]() ,0)如图(5)
,0)如图(5)
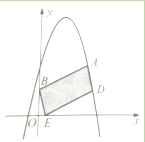

图4 图5 图6
【解析】(1)将A(2,2)代入y=![]() x+n从而求出直线解析式,将抛物线解析式设成顶点坐标y=a
x+n从而求出直线解析式,将抛物线解析式设成顶点坐标y=a![]() +4代入A(2,2)从而求出抛物线解析式。
+4代入A(2,2)从而求出抛物线解析式。
(2)如图1,设PP′与AC的交点为H,作HM⊥x轴于M,作PN⊥HM于N;由题意可列出方程组m=-2![]() +4x ①;4x=3m-2 ②,联立即可得出答案。
+4x ①;4x=3m-2 ②,联立即可得出答案。
(3)设点E坐标为(t,0),以AB为边或对角线进行分类讨论即可得出答案。
【考点精析】解答此题的关键在于理解两点间的距离的相关知识,掌握同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取 ![]() =1.732,结果精确到1m)
=1.732,结果精确到1m)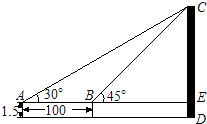
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学十分重视中学生的用眼卫生,并定期进行视力检测.某次检测设有A、B两处检测点,甲、乙、丙三名学生各自随机选择其中的一处检测视力.
(1)求甲、乙、丙三名学生在同一处检测视力的概率;
(2)求甲、乙、丙三名学生中至少有两人在B处检测视力的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F. 
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班 ![]() 名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如下:
名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如下:
自选项目 | 人数 | 频率 |
立定跳远 | 9 | 0.18 |
三级蛙跳 | 12 |
|
一分钟跳绳 | 8 | 0.16 |
投掷实心球 |
| 0.32 |
推铅球 | 5 | 0.1 |
合计 | 50 | 1 |
(1)求 ![]() 的值;
的值;
(2)若将各自选项目的人数所占比例绘制成扇形统计图,求“一分钟跳绳”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生.为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至多有一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公交总站(A点)与B、C两个站点的位置如图所示,已知AC=6km,∠B=30°,∠C=15°,求B站点离公交总站的距离即AB的长(结果保留根号). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李师傅加工1个甲种零件和1个乙种零件的时间分别是固定的,现知道李师傅加工3个甲种零件和5个乙种零件共需55分钟;加工4个甲种零件和9个乙种零件共需85分钟,则李师傅加工2个甲种零件和4个乙种零件共需分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣ ![]() x+1的图象与x轴、y轴分别交于点A、B,把Rt△AOB绕点A顺时针旋转角α(30°<α<180°),得到△AO′B′.
x+1的图象与x轴、y轴分别交于点A、B,把Rt△AOB绕点A顺时针旋转角α(30°<α<180°),得到△AO′B′. 
(1)当α=60°时,判断点B是否在直线O′B′上,并说明理由;
(2)连接OO′,设OO′与AB交于点D,当α为何值时,四边形ADO′B′是平行四边形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com